Form finding in elastic gridshells

Abstract

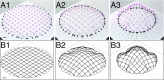
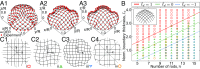
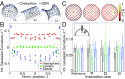
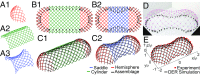
Elastic gridshells comprise an initially planar network of elastic rods that are actuated into a shell-like structure by loading their extremities. The resulting actuated form derives from the elastic buckling of the rods subjected to inextensibility. We study elastic gridshells with a focus on the rational design of the final shapes. Our precision desktop experiments exhibit complex geometries, even from seemingly simple initial configurations and actuation processes. The numerical simulations capture this nonintuitive behavior with excellent quantitative agreement, allowing for an exploration of parameter space that reveals multistable states. We then turn to the theory of smooth Chebyshev nets to address the inverse design of hemispherical elastic gridshells. The results suggest that rod inextensibility, not elastic response, dictates the zeroth-order shape of an actuated elastic gridshell. As it turns out, this is the shape of a common household strainer. Therefore, the geometry of Chebyshev nets can be further used to understand elastic gridshells. In particular, we introduce a way to quantify the intrinsic shape of the empty, but enclosed regions, which we then use to rationalize the nonlocal deformation of elastic gridshells to point loading. This justifies the observed difficulty in form finding. Nevertheless, we close with an exploration of concatenating multiple elastic gridshell building blocks.

Keywords: Chebyshev nets; buckling; elastic structures; gridshells; mechanical instabilities.

Fig. 1.

(A and B) Actuation of an elastic gridshell from (A) experiments and (B) DER simulation. The edge points of a planar and unloaded footprint (A1 and B1) are gradually moved toward a prescribed actuated boundary (A2 and B2) to yield an actuated shape (A3 and B3). (Scale bar, 20 mm.)

Fig. 2.

Elastic gridshells with circular boundaries. (A) Multistable states of a circular elastic gridshell with $({\overline{L}}_d,n)=(0.8,12)$ observed from experiments (red solid circles) and simulations (black lines). (B) Phase diagram of elastic gridshells with circular boundaries. In addition to the three states in A, a convex dome-shaped state (B, Inset) is obtained by extending the legs. Each data point is obtained from DER simulations under a jittering procedure. (C) Four representative modes of the circular elastic gridshells with different symmetry properties.

Fig. 3.

Hemispherical elastic gridshells from Chebyshev’s hemisphere ansatz. (A) Photograph of a nearly hemispherical gridshell. (B) Boundary of the hemisphere domain (outermost contour) and spherical caps (five inner contours) obtained by cutting with planes (Inset). (C) Positions of the joints (red solid circles; 3D scanning), along with the corresponding DER simulation (black solid lines) and the $d$-sampled Chebyshev net (blue solid lines). (D) Spherical-cap elastic gridshells obtained from DER simulations, whose footprints are shown in B. Colorbar represents deviation from the $d$-sampled Chebyshev net normalized by the radius of the sphere, $\overline{e}=\mathrm{\Delta }/\rho$. (E and F) A household strainer of $z^{\ast }/\rho =0.28$ (E) and its flattened 2D domain (F), showing excellent agreement with a Chebyshev domain (solid line).

Fig. 4.

Notion of integrated Gauss curvature. (A) Elastic gridshells (DER simulation; black solid lines) and their $d$-sampled Chebyshev ansatzes (blue solid lines), which are from Left to Right, respectively, a hemisphere, a cylinder, and a saddle (each with half-span $L$). (B) Distribution of $K^{\square }$, the integrated Gauss curvature of a unit cell obtained from Eq. 2, for three elastic gridshells. Each unit cell is positioned by its normalized centroid $\overline{x}=x/L$. (C) Three indentation cases of an actuated hemispherical gridshell: (Left) inward and (Center) outward normal displacement at the north pole and (Right) inward displacement at $\pi /4$ latitude and longitude. The normalized displacement field is $|𝐮|/{\delta }_{\mathrm{o}}$. (D) Binned $K^{\square }$ for C (Left to Right). Averages (bins) and standard deviations (error bars) show the spatial heterogeneity (i.e., nonlocality) of the shearing response.

Fig. 5.

Elastic gridshells from building blocks. (A) Pruned elastic gridshell building blocks: (A1) hemisphere, (A2) cylinder, and (A3) saddle. (B and C) Comparison of concatenated elastic gridshell assemblage (black solid lines) and its building blocks (colored solid lines) for (B1 and C1) stadium (A1-A2-A1) and (B2 and C2) peanut (A1-A3-A1). (D) Photograph of a peanut-shaped elastic gridshell. (E) Positions of the joints (red solid circles; 3D scanning), along with the corresponding DER simulation (black solid lines).