Computation of extreme heat waves in climate models using a large deviation algorithm

Abstract

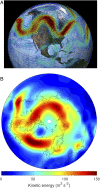
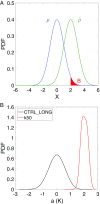
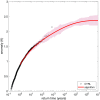
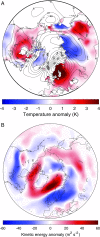
Studying extreme events and how they evolve in a changing climate is one of the most important current scientific challenges. Starting from complex climate models, a key difficulty is to be able to run long enough simulations to observe those extremely rare events. In physics, chemistry, and biology, rare event algorithms have recently been developed to compute probabilities of events that cannot be observed in direct numerical simulations. Here we propose such an algorithm, specifically designed for extreme heat or cold waves, based on statistical physics. This approach gives an improvement of more than two orders of magnitude in the sampling efficiency. We describe the dynamics of events that would not be observed otherwise. We show that European extreme heat waves are related to a global teleconnection pattern involving North America and Asia. This tool opens up a wide range of possible studies to quantitatively assess the impact of climate change.

Keywords: climate extremes; heat waves; large deviation theory; rare event algorithms; statistical physics.

Fig. 1.

(A) Snapshot of wind speed velocity at the top of the troposphere, showing the jet stream over North America (image courtesy of NASA/Goddard Space Flight Center Scientific Visualization Studio). (B) Average horizontal kinetic energy at 500 hPa (midtroposphere) in the Plasim model, showing the averaged Northern Hemisphere jet stream.

Fig. 2.

(A) The red color marks the area of Europe over which the temperature is averaged. (B) Time series of European surface temperature anomaly, 6 h (light blue) and 90 d running mean (dark blue), during 360 d and $\mathrm{1,000}$ y (Inset). The red triangles and circles feature one local maximum of the temperature anomalies, as an example of a $2\text{K}$ heat wave lasting $90$ d.

Fig. 3.

(A) We want to estimate the probability to be in the set $B$, for the model PDF $\rho (x)$. We are able to sample instead from the PDF $\stackrel{\sim }{\rho }(x)$ for which the rare event becomes common. We know the relation $L=\rho /\stackrel{\sim }{\rho }$ and can recover the model statistics $\rho$, from the importance sampling $\stackrel{\sim }{\rho }$. (B) PDF of the time-averaged temperature $a$ ($T=90\text{d}$) for the model control run (black) and for the algorithm statistics with $k=50$, illustrating that the algorithm performs importance sampling and that +2 K heat waves become common for the algorithm while they are rare for the model.

Fig. 4.

Return times for the $90$-d Europe surface temperature, computed from the $\mathrm{1,000}$-y-long control run (black) and from the large deviation algorithm, at the same computational cost as the control run (red). This illustrates both the good overlap on the 10- to 300-y range and the fact that the algorithm can predict probability for events that cannot be observed in the control run.

Fig. 5.

(A) Northern Hemisphere surface temperature anomaly (colors) and 500-hPa geopotential height anomaly (contours), conditional on the occurrence of heat wave conditions $\frac{1}{T}{\int }_0^{T}A(x_n(t))dt>a$, with $T=90\text{d}$ and a = 2 K, estimated from the large deviation algorithm. (B) Northern Hemisphere anomaly of the averaged kinetic energy for the zonal velocity at 500 hPa conditional on the occurrence of heat wave conditions $𝔼\left[K{E}_{500}\mid \frac{1}{T}{\int }_0^{T}A(x_n(t))dt>a\right]$, with $T=90\text{d}$ and a = 2 K, estimated from the large deviation algorithm, with respect to the long-time average $𝔼\left[K{E}_{500}\right]$ computed from the control run.