Age-based partitioning of individual genomic inbreeding levels in Belgian Blue cattle

Abstract

Background: Inbreeding coefficients can be estimated either from pedigree data or from genomic data, and with genomic data, they are either global or local (when the linkage map is used). Recently, we developed a new hidden Markov model (HMM) that estimates probabilities of homozygosity-by-descent (HBD) at each marker position and automatically partitions autozygosity in multiple age-related classes (based on the length of HBD segments). Our objectives were to: (1) characterize inbreeding with our model in an intensively selected population such as the Belgian Blue Beef (BBB) cattle breed; (2) compare the properties of the model at different marker densities; and (3) compare our model with other methods.

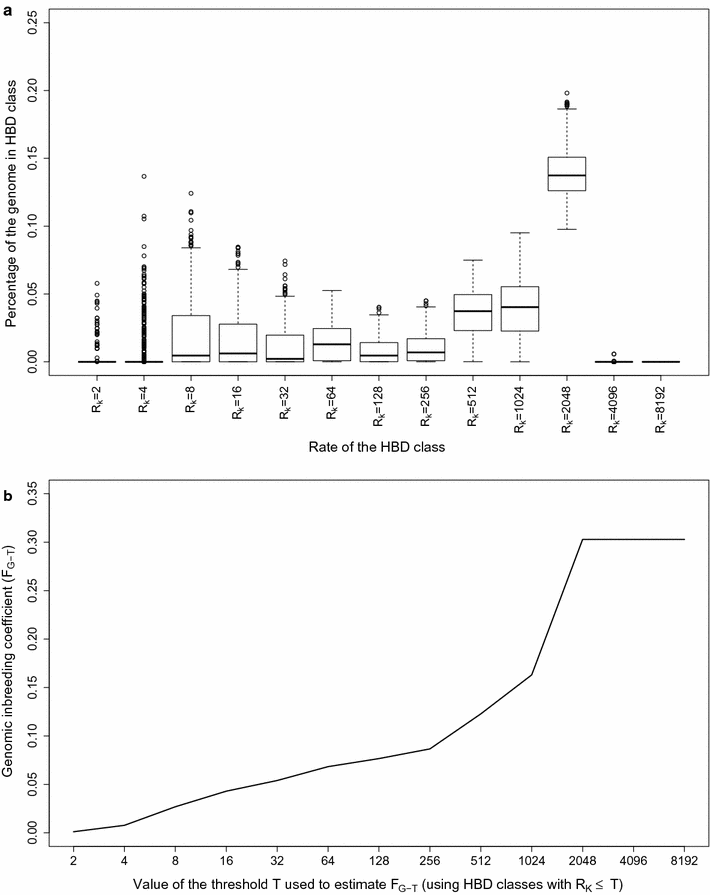
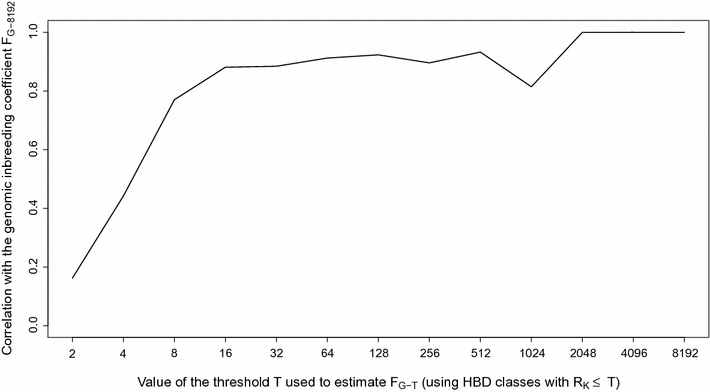
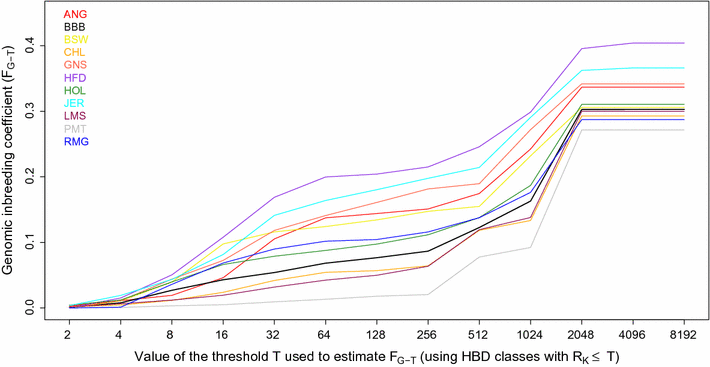
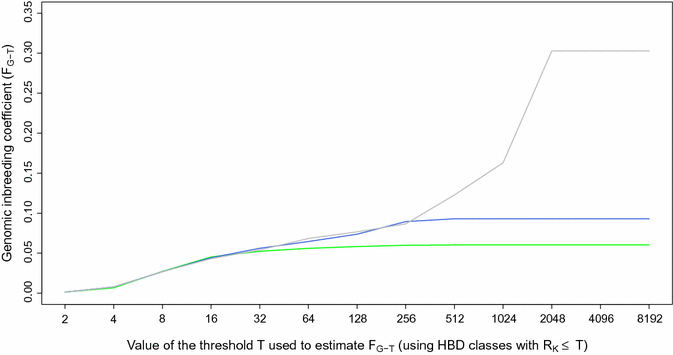
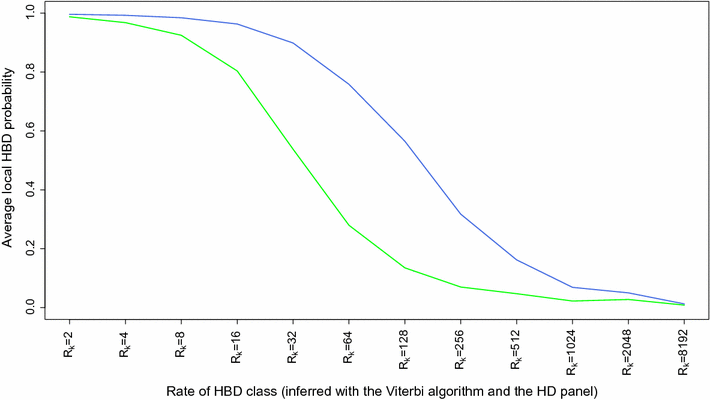
Results: When using 600 K single nucleotide polymorphisms (SNPs), the inbreeding coefficient (probability of sampling an HBD locus in an individual) was on average 0.303 (ranging from 0.258 to 0.375). HBD-classes associated to historical ancestors (with small segments ≤ 200 kb) accounted for 21.6% of the genome length (71.4% of the total length of the genome in HBD segments), whereas classes associated to more recent ancestors accounted for only 22.6% of the total length of the genome in HBD segments. However, these recent classes presented more individual variation than more ancient classes. Although inbreeding coefficients obtained with low SNP densities (7 and 32 K) were much lower (0.060 and 0.093), they were highly correlated with those obtained at higher density (r = 0.934 and 0.975, respectively), indicating that they captured most of the individual variation. At higher SNP density, smaller HBD segments are identified and, thus, more past generations can be explored. We observed very high correlations between our estimates and those based on homozygosity (r = 0.95) or on runs-of-homozygosity (r = 0.95). As expected, pedigree-based estimates were mainly correlated with recent HBD-classes (r = 0.56).

Conclusions: Although we observed high levels of autozygosity associated with small HBD segments in BBB cattle, recent inbreeding accounted for most of the individual variation. Recent autozygosity can be captured efficiently with low-density SNP arrays and relatively simple models (e.g., two HBD classes). The HMM framework provides local HBD probabilities that are still useful at lower SNP densities.

Fig. 1

Partitioning of genome-wide autozygosity for the 634 Belgian Blue sires using the BovineHD SNP panel. a Boxplot of percentages of individual genomes associated with 13 HBD-classes with pre-defined R _k rates (Mix14R model). The percentages correspond to individual genome-wide probabilities of belonging to each of the HBD-classes. b Genomic inbreeding coefficients estimated with respect to different base populations (F _G-T) obtained by selecting different thresholds T that determine which HBD-classes are considered in the estimation of F _G-T (e.g., setting the base population approximately 0.5 * T generations in the past). The corresponding inbreeding coefficients F _G-T are estimated as the probability of belonging to any of the HBD classes with a R _k ≤ T averaged over the whole genome

Fig. 2

Correlations between genomic inbreeding coefficients estimated with respect to different base populations (F _G-T) and the inbreeding coefficient estimated with the most remote base population F_G-8192 (including all HBD classes). Different base populations are obtained by selecting different thresholds T that determine which HBD-classes are considered in the estimation of F _G-T (e.g., setting the base population approximately 0.5 * T generations in the past). The corresponding inbreeding coefficients F _G-T are estimated as the probability of belonging to any of the HBD classes with a R _k ≤ T averaged over the whole genome. Estimation of inbreeding coefficients was performed with the Mix14R model (13 HBD-classes model with pre-defined R _k rates) for 634 Belgian Blue sires and using the BovineHD SNP panel

Fig. 3

Estimation of inbreeding coefficients with respect to different base populations (the threshold T determines which HBD classes are included in the estimation of F _G-T) with a Mix14R model in 11 cattle breeds of European origin using the BovineHD SNP panel. ANG Angus, BBB Belgian Blue Beef cattle, BSW Brown Swiss, CHL Charolais, GNS Guernsey, HFD Hereford, HOL Holstein, JER Jersey, LMS Limousin, PMT Piedmontese, RMG Romagnola

Fig. 4

Comparison of inbreeding coefficients estimated with different SNP densities (LD panel in green, 50 K panel in blue and BovineHD panel in grey) and for different base populations (the threshold T determines which HBD classes are included in the estimation of F _G-T). Estimation of inbreeding coefficients was performed with the Mix14R model for 634 Belgian Blue sires

Fig. 5

Illustrations of the identification of HBD segments using different SNP panels. a Example of estimated HBD probabilities for one individual on Bos taurus autosome (BTA) 16 using different SNP densities (LD panel in green, 50 K panel in blue and BovineHD panel in grey). The horizontal lines below the curves represent HBD segments as identified by the Viterbi algorithm with the three panels. An extremely long HBD segment (~ 50 Mb) is represented (there are only 69 such HBD segments identified in the entire data set), suggesting recent inbreeding. This bull is one of the 29 individuals carrying such long HBD segments and has a pedigree inbreeding coefficient of 0.048. b Comparisons of HBD segments identified for 50 individuals on BTA5 using different panels (each line represents one individual). Segments identified with the HD, 50 K and LD panels are represented in grey, blue and green, respectively (with lower density results masking results obtained at higher density). The shortest HBD segments are identified with the HD panel (indicated in grey) whereas those of intermediate size are also captured with the 50 K panel (and still missed with the LD panel) and indicated in blue. For a few HBD segments, the use of the LD panel results in longer segments

Fig. 6

Average HBD probabilities estimated for HBD segments associated with different age-based classes. HBD probabilities were estimated with the LD (green) or 50 K (blue) panels whereas the age-based classes were determined by using the Viterbi algorithm and the HD panel (a 20-fold SNP density increase). The average HBD probabilities indicate whether segments from different classes are captured using lower density panels

Fig. 7

Comparison of the length of HBD segments identified with WGS data and with the 1R or the Mix14R models on BTA3. The grey and red lines represent the HBD probabilities estimated with the 1R and Mix14R models, respectively; the dark grey dots represent the probability of heterozygous genotypes (obtained from the VCF); the blue and yellow segments represent HBD segments identified with the Viterbi algorithm with the 1R and the Mix14R model, respectively

Fig. 8

Correlations between the inbreeding coefficients estimated with respect to different base populations (F _G-T) and the inbreeding coefficient estimated from pedigree data for the Belgian Blue sires born after 1999 and using the HD panel. Different base populations were obtained by selecting different thresholds T that determine which HBD-classes are considered for estimating F _G-T (e.g., setting the base population approximately 0.5 * T generations in the past). The corresponding inbreeding coefficients F _G-T are estimated as the probability of belonging to any of the HBD classes with a R _k ≤ T averaged over the whole genome. Genomic inbreeding coefficients were estimated with the Mix14R model