Optical coherence elastography in ophthalmology
- PMID: 29275544
- PMCID: PMC5745712
- DOI: 10.1117/1.JBO.22.12.121720
Optical coherence elastography in ophthalmology
Abstract
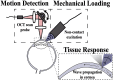
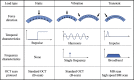
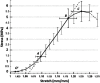
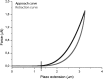
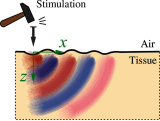
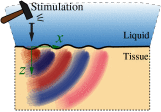
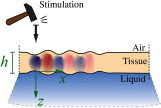
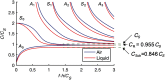
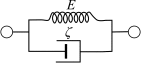
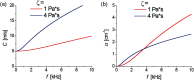
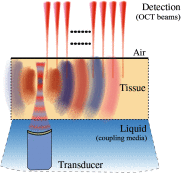
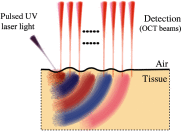
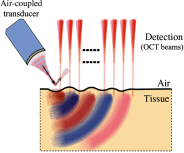
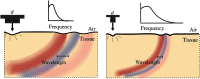
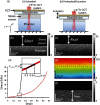
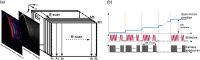
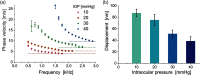
Optical coherence elastography (OCE) can provide clinically valuable information based on local measurements of tissue stiffness. Improved light sources and scanning methods in optical coherence tomography (OCT) have led to rapid growth in systems for high-resolution, quantitative elastography using imaged displacements and strains within soft tissue to infer local mechanical properties. We describe in some detail the physical processes underlying tissue mechanical response based on static and dynamic displacement methods. Namely, the assumptions commonly used to interpret displacement and strain measurements in terms of tissue elasticity for static OCE and propagating wave modes in dynamic OCE are discussed with the ultimate focus on OCT system design for ophthalmic applications. Practical OCT motion-tracking methods used to map tissue elasticity are also presented to fully describe technical developments in OCE, particularly noting those focused on the anterior segment of the eye. Clinical issues and future directions are discussed in the hope that OCE techniques will rapidly move forward to translational studies and clinical applications.
Keywords: air-coupled ultrasound; mechanical wave imaging; ocular biomechanics; optical coherence elastography, acoustic radiation force; optical coherence tomography; phase-sensitive optical coherence tomography; speckle tracking; tissue elasticity.
(2017) COPYRIGHT Society of Photo-Optical Instrumentation Engineers (SPIE).
Figures
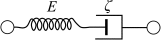






Similar articles
-
Anterior segment applications of optical coherence elastography in ophthalmic and vision science: a systematic review of intrinsic measurement techniques and clinical relevance.Prog Biomed Eng (Bristol). 2025 May 15;7(3). doi: 10.1088/2516-1091/add4d9. Prog Biomed Eng (Bristol). 2025. PMID: 40328290
-
Strain and elasticity imaging in compression optical coherence elastography: The two-decade perspective and recent advances.J Biophotonics. 2021 Feb;14(2):e202000257. doi: 10.1002/jbio.202000257. Epub 2020 Nov 3. J Biophotonics. 2021. PMID: 32749033 Review.
-
Optical coherence elastography and its applications for the biomechanical characterization of tissues.J Biophotonics. 2023 Dec;16(12):e202300292. doi: 10.1002/jbio.202300292. Epub 2023 Oct 9. J Biophotonics. 2023. PMID: 37774137 Review.
-
Acoustic radiation force optical coherence elastography for elasticity assessment of soft tissues.Appl Spectrosc Rev. 2019;54(6):457-481. doi: 10.1080/05704928.2018.1467436. Epub 2018 Jun 25. Appl Spectrosc Rev. 2019. PMID: 31749516 Free PMC article.
-
Digital image correlation-based optical coherence elastography.J Biomed Opt. 2013 Dec;18(12):121515. doi: 10.1117/1.JBO.18.12.121515. J Biomed Opt. 2013. PMID: 24346855
Cited by
-
VP-net: an end-to-end deep learning network for elastic wave velocity prediction in human skin in vivo using optical coherence elastography.Front Bioeng Biotechnol. 2024 Oct 14;12:1465823. doi: 10.3389/fbioe.2024.1465823. eCollection 2024. Front Bioeng Biotechnol. 2024. PMID: 39469517 Free PMC article.
-
Delineating Corneal Elastic Anisotropy in a Porcine Model Using Noncontact OCT Elastography and Ex Vivo Mechanical Tests.Ophthalmol Sci. 2021 Sep 22;1(4):100058. doi: 10.1016/j.xops.2021.100058. eCollection 2021 Dec. Ophthalmol Sci. 2021. PMID: 36246948 Free PMC article.
-
Adaptive contour-tracking to aid wide-field swept-source optical coherence tomography imaging of large objects with uneven surface topology.Biomed Opt Express. 2024 Jul 29;15(8):4891-4908. doi: 10.1364/BOE.533399. eCollection 2024 Aug 1. Biomed Opt Express. 2024. PMID: 39347000 Free PMC article.
-
Quantitative assessment of corneal biomechanical changes in vivo after photorefractive intrastromal corneal cross-linking using optical coherence elastography.Quant Imaging Med Surg. 2024 Oct 1;14(10):7640-7653. doi: 10.21037/qims-24-590. Epub 2024 Sep 26. Quant Imaging Med Surg. 2024. PMID: 39429567 Free PMC article.
-
In vivo corneal elastography: A topical review of challenges and opportunities.Comput Struct Biotechnol J. 2023 Apr 13;21:2664-2687. doi: 10.1016/j.csbj.2023.04.009. eCollection 2023. Comput Struct Biotechnol J. 2023. PMID: 37181662 Free PMC article. Review.
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

