Susceptibility-induced distortion that varies due to motion: Correction in diffusion MR without acquiring additional data
- PMID: 29277648
- PMCID: PMC5883370
- DOI: 10.1016/j.neuroimage.2017.12.040
Susceptibility-induced distortion that varies due to motion: Correction in diffusion MR without acquiring additional data
Abstract
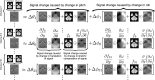
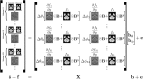
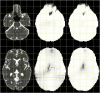
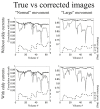
Because of their low bandwidth in the phase-encode (PE) direction, the susceptibility-induced off-resonance field causes distortions in echo planar imaging (EPI) images. It is therefore crucial to correct for susceptibility-induced distortions when performing diffusion studies using EPI. The susceptibility-induced field is caused by the object (head) disrupting the field and it is typically assumed that it remains constant within a framework defined by the object, (i.e. it follows the object as it moves in the scanner). However, this is only approximately true. When a non-spherical object rotates around an axis other than that parallel with the magnetic flux (the z-axis) it changes the way it disrupts the field, leading to different distortions. Hence, if using a single field to correct for distortions there will be residual distortions in the volumes where the object orientation is substantially different to that when the field was measured. In this paper we present a post-processing method for estimating the field as it changes with motion during the course of an experiment. It only requires a single measured field and knowledge of the orientation of the subject when that field was acquired. The volume-to-volume changes of the field as a consequence of subject movement are estimated directly from the diffusion data without the need for any additional or special acquisitions. It uses a generative model that predicts how each volume would look predicated on field change and inverts that model to yield an estimate of the field changes. It has been validated on both simulations and experimental data. The results show that we are able to track the field with high accuracy and that we are able to correct the data for the adverse effects of the changing field.
Keywords: Diffusion; Dynamic; Movement; Registration; Susceptibility.
Copyright © 2017 The Authors. Published by Elsevier Inc. All rights reserved.
Figures




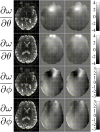
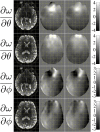
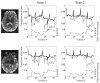

References
-
- Andersson J.L.R., Hutton C., Ashburner J., Turner R., Friston K. Modelling geometric deformations in EPI time series. Neuroimage. 2001;13:903–919. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

