Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2017 Dec 26;18(1):48.
doi: 10.3390/s18010048.

Research on Ship-Radiated Noise Denoising Using Secondary Variational Mode Decomposition and Correlation Coefficient

Yuxing Li  1 , Yaan Li  2 , Xiao Chen  3 , Jing Yu  4
Affiliations

Research on Ship-Radiated Noise Denoising Using Secondary Variational Mode Decomposition and Correlation Coefficient

Yuxing Li et al. Sensors (Basel). .

Abstract

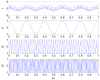
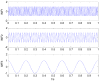
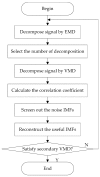
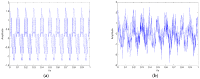
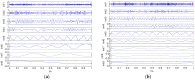
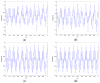
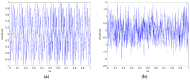
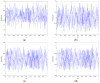
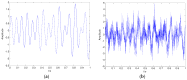
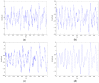
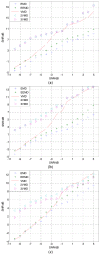
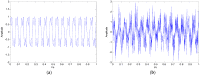
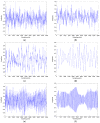
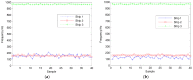
As the sound signal of ships obtained by sensors contains other many significant characteristics of ships and called ship-radiated noise (SN), research into a denoising algorithm and its application has obtained great significance. Using the advantage of variational mode decomposition (VMD) combined with the correlation coefficient for denoising, a hybrid secondary denoising algorithm is proposed using secondary VMD combined with a correlation coefficient (CC). First, different kinds of simulation signals are decomposed into several bandwidth-limited intrinsic mode functions (IMFs) using VMD, where the decomposition number by VMD is equal to the number by empirical mode decomposition (EMD); then, the CCs between the IMFs and the simulation signal are calculated respectively. The noise IMFs are identified by the CC threshold and the rest of the IMFs are reconstructed in order to realize the first denoising process. Finally, secondary denoising of the simulation signal can be accomplished by repeating the above steps of decomposition, screening and reconstruction. The final denoising result is determined according to the CC threshold. The denoising effect is compared under the different signal-to-noise ratio and the time of decomposition by VMD. Experimental results show the validity of the proposed denoising algorithm using secondary VMD (2VMD) combined with CC compared to EMD denoising, ensemble EMD (EEMD) denoising, VMD denoising and cubic VMD (3VMD) denoising, as well as two denoising algorithms presented recently. The proposed denoising algorithm is applied to feature extraction and classification for SN signals, which can effectively improve the recognition rate of different kinds of ships.

Keywords: correlation coefficient (CC); denoising; secondary variational mode decomposition (2VMD); ship-radiated noise (SN); variational mode decomposition (VMD).

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Simulation signals.
Figure 2
Figure 2
Decomposition result by variational mode decomposition (VMD).
Figure 3
Figure 3
The flow chart of proposed secondary variational mode decomposition (2VMD) denoising algorithm.
Figure 4
Figure 4
(a) The clear signal; (b) the noisy signal.
Figure 5
Figure 5
The decomposition result of empirical mode decomposition (EMD), ensemble EMD (EEMD), VMD and 2VMD for the noisy signal. (a) EMD; (b) EEMD; (c) VMD; (d) 2VMD.
Figure 5
Figure 5
The decomposition result of empirical mode decomposition (EMD), ensemble EMD (EEMD), VMD and 2VMD for the noisy signal. (a) EMD; (b) EEMD; (c) VMD; (d) 2VMD.
Figure 6
Figure 6
The denoising results of EMD, EEMD, VMD and 2VMD for the noisy signal. (a) EMD; (b) EEMD; (c) VMD; (d) 2VMD.
Figure 7
Figure 7
The time-domain waveform for the clear signal and noisy signal. (a) The clear signal; (b) the noisy signal.
Figure 8
Figure 8
The denoising results of EMD, EEMD, VMD and 2VMD for the noisy signal. (a) EMD; (b) EEMD; (c) VMD; (d) 2VMD.
Figure 9
Figure 9
(a) The clear signal; (b) the noisy signal.
Figure 10
Figure 10
The denoising results of EMD, EEMD, VMD and 2VMD for the noisy signal. (a) EMD; (b) EEMD; (c) VMD; (d) 2VMD.
Figure 11
Figure 11
The denoising results of EMD, EEMD, VMD, 2VMD and cubic VMD (3VMD) for different simulation signals. (a) The denoising results of simulation 1; (b) the denoising results of simulation 2; (c) the denoising results of simulation 3.
Figure 12
Figure 12
(a) The clear signal; (b) the noisy signal.
Figure 13
Figure 13
Three kinds of ship-radiated noise (SN). (a) Ship 1 without denoising; (b) Ship 1 after denoising; (c) Ship 2 without denoising; (d) Ship 2 after denoising; (e) Ship 3 without denoising; (f) Ship 3 after denoising.
Figure 14
Figure 14
The center frequency of the IMF with the highest energy (EIMF). (a) without denoising; (b) after denoising.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Guo X., Shen C., Chen L. Deep Fault Recognizer: An Integrated Model to Denoise and Extract Features for Fault Diagnosis in Rotating Machinery. Appl. Sci. 2017;7:41. doi: 10.3390/app7010041. - DOI
    1. Siddagangaiah S., Li Y., Guo X., Yang K. On the dynamics of ocean ambient noise: Two decades later. Chaos. 2015;25:103117. doi: 10.1063/1.4932561. - DOI - PubMed
    1. Murguia J.S., Campos C.E. Wavelet analysis of chaotic time series. Rev. Mex. Fis. 2006;52:155–162.
    1. Liu Y.X., Yang G.S., Jia Q. Adaptive Noise Reduction for Chaotic Signals Based on Dual-Lifting Wavelet Transform. Acta Electron. Sin. 2011;39:13–17.
    1. Zhang L., Bao P., Wu X. Multiscale LMMSE-based image denoising with optimal wavelet selection. IEEE Trans. Circuits Syst. Video Technol. 2005;15:469–481. doi: 10.1109/TCSVT.2005.844456. - DOI

LinkOut - more resources