Design strategies for dynamic closed-loop optogenetic neurocontrol in vivo

Abstract

Objective: Controlling neural activity enables the possibility of manipulating sensory perception, cognitive processes, and body movement, in addition to providing a powerful framework for functionally disentangling the neural circuits that underlie these complex phenomena. Over the last decade, optogenetic stimulation has become an increasingly important and powerful tool for understanding neural circuit function, owing to the ability to target specific cell types and bidirectionally modulate neural activity. To date, most stimulation has been provided in open-loop or in an on/off closed-loop fashion, where previously-determined stimulation is triggered by an event. Here, we describe and demonstrate a design approach for precise optogenetic control of neuronal firing rate modulation using feedback to guide stimulation continuously.

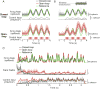
Approach: Using the rodent somatosensory thalamus as an experimental testbed for realizing desired time-varying patterns of firing rate modulation, we utilized a moving average exponential filter to estimate firing rate online from single-unit spiking measured extracellularly. This estimate of instantaneous rate served as feedback for a proportional integral (PI) controller, which was designed during the experiment based on a linear-nonlinear Poisson (LNP) model of the neuronal response to light.

Main results: The LNP model fit during the experiment enabled robust closed-loop control, resulting in good tracking of sinusoidal and non-sinusoidal targets, and rejection of unmeasured disturbances. Closed-loop control also enabled manipulation of trial-to-trial variability.

Significance: Because neuroscientists are faced with the challenge of dissecting the functions of circuit components, the ability to maintain control of a region of interest in spite of changes in ongoing neural activity will be important for disambiguating function within networks. Closed-loop stimulation strategies are ideal for control that is robust to such changes, and the employment of continuous feedback to adjust stimulation in real-time can improve the quality of data collected using optogenetic manipulation.

Figure 1. Closed loop optogenetic control of firing rate

(A) Physical diagram. (B) System block flow diagram. (C) Procedure for closed-loop stimulation experiments. The observer was designed for a given reference firing rate pattern previous to experiments. A model was fit to data recorded for system identification during the experiment. Using this model, controller gains were optimized in simulation. These parameters were then used for experimental closed-loop stimulation.

Figure 2. Closed- vs. open-loop optogenetic control of dynamic firing rate trajectories

(A) Closed- and open-loop control of sinusoidally-modulated firing rate. Closed-loop (black) control and pulsatile open-loop (red) stimulation were used to elicit a 1 Hz sinusoidally modulated firing rate. Light lines correspond to single trial firing rates estimated by smoothing spike trains with a Gaussian window (120 ms SD); bold lines are the trial-averaged rate. Average control inputs (i.e., light) are below the corresponding firing rate trajectory. (B) Closed- and open-loop control in presence of a disturbance. Control was challenged with a whisker disturbance at 2 seconds into the control epoch, as shown in gray (top). (C) Closed-loop and open-loop control of non-sinusoidal firing rate. Top, firing rates for closed-loop (black) vs. open-loop (red) control: average in bold, while fills represent 95% confidence intervals for smoothed PSTH. Middle, Fano factor calculated in 250-ms sliding window for closed- and open-loop control (n = 25 trials). Bottom, trial-averaged control inputs for closed-loop (black) or open-loop (red).

Figure 3. Observer design: Choosing filter bandwidth

(A) Conceptual diagram. A given sinusoidal firing rate (λ) drove a Poisson spike generator (P). Tire resulting spike train was multiplied by Δ⁻¹ (not shown) ahead of filtering. Filters parameterized by a time constant, τ, yielded an estimate of the true rate. (B) Optimal time constant as a function of expected number of spikes per period and degree of modulation about mean (top) and as a function of z (bottom). For visualization, the optimal filter has been normalized by the frequency of each sinusoid. Fit: a = 0.423, b = 0.389. (C) Filter time constants designed for single-trial estimation where μ = 20 spikes/s, σ/μ = 1. Bold purple, region of frequencies where the derived design equation was fit. Light purple, frequencies at which the the design equation was extrapolated (z < 12). Insets, example single-trial estimates (purple) of the ground truth rate (green) at indicated modulation frequencies.

Figure 4. Controller Design: Tuning the controller around an LNP model neuron

(A) Controller design through simulation. The closed-loop system was simulated with a model of the neural system for design purposes. (B) Example tuning surface for 5 Hz sinusoidal trajectory. In simulation, the controller was tasked with tracking a sinusoidal trajectory (here, 5 Hz), using the observer designed previously for the corresponding reference. The objective was to minimize the squared tracking error, weighted as a function of frequencies important for the control task. (C) Examples of optimal and suboptimal controller gains. Frequency-domain error (top row) corresponds to amplitude of error between the raw instantaneous rate (n/Δ) and the reference at DC and the modulation frequency (here, 5 Hz). For comparison, the square root of the frequency-weighted squared error (J_fwt) is also provided. Error bars correspond to +1 SD. Corresponding error spectra are provided (middle row), as compared to a simulated Poisson process modulated at the reference rate (light grey). Green lines highlight DC and f_mod Finally, time-domain tracking is provided (bottom).

Figure 5. LNP Model Performance: Open-loop vs. closed-loop

(A) Fitting the linear-nonlinear (LN) model. (B) A typical LN model fit to training data. Left, the linear system estimated using whitened spike triggered averaging; error bars correspond to +/− 1 SD for the lagged coefficients of the kernel when fit to 10 subsets of the full training dataset. Right, the static nonlinearity fit by maximum likelihood, given the observed spikes. Gray points indicate the experimental firing rate (PSTH smoothed with 1-ms Gaussian) versus the kernel-filtered stimulus. (C) LNP prediction of response to open-loop ‘replay’ of stimulation used experimentally during a 5 Hz sinusoidal control task, using the same LN model shown in B. Top, firing rate predicted by the model (red) as compared to the experimental data for the same cell (black); bottom, experimental optical input. (D) LNP prediction of response to simulated closed-loop stimulation. Firing rate and light input predicted by the model (blue) as compared to the experimental data for the same cell (black); bottom, simulated (blue) and experimental (black) closed-loop stimulation

Figure 6. Robustness of Control to Model Inaccuracy

(A) Model Perturbation and Simulation. Tire static gain (g) and tire bias (m) of tire linear component of tire LNP model were systematically perturbed and simulated either in closed- or open-loop. (B) Grid Search Over Gain and Bias. Fractional changes in g and m ranged from five times smaller to five times greater than the original parameter value. Grayscale represents the percentage change in tracking performance (J_fwt) between that of the original model and each perturbed version. This tracking error was calculated from 1 second onward for 5-second control epochs. (C) Changing Bias. Holding all else constant, m was changed, and the tracking performance was quantified for closed-loop control vs. open-loop replay of the light traces used to stimulate the original neuron. Gray circles indicate the estimated biases of all recorded neurons relative to the model used for perturbation study (n=20). (D) Examples of Simulated Control When Bias Estimation Inaccurate. (Top) Outcome when the actual neuron (blue) was 2 times less biased than the model around which controller were tuned (black); (Bottom) the outcome when the actual neuron (blue) was 2 times more negatively biased than the model around which the controller was tuned (black). Scale bar indicates 20 spikes/s. (E) Changing Gain. Holding all else constant, g was changed and the tracking performance quantified for closed-loop control vs. open-loop replay of the light traces used to stimulate the original neuron. Gray circles indicate the estimated gains of all recorded neurons relative to the model used for perturbation study (n=20). (F) Examples of Simulated Control When Gain Estimation Inaccurate. (Top) Outcome when the actual neuron (blue) was 2 times less sensitive than the model around which controller were tuned (black); (Bottom) the outcome when the actual neuron (blue) was 2 times more sensitive than the model around which the controller was tuned (black). Scale bar indicates 20 spikes/s

Figure 7. Sinusoidal tracking performance

(A) Example experimental implementation (“Cell 3”) where the controller and observer were tuned for a trajectory modulated at 5 Hz. The third of a five-second control epoch is shown. (B) Population performance for tracking a 5 Hz sinusoidal tra jectory (LNP prediction vs. experimental): average (black bar) and individual cells (colored symbols). 95% confidence intervals for this metric were calculated for simulated Poisson firing at the reference rate and plotted in light grey. Left, results of design procedure predicted by the LNP models fit and tuned around during the experiment. Middle, experimental closed-loop tracking performance. Right, experimental open-loop tracking performance. (C) Closed- vs. open-loop experimental performance on 1, 5, & 10 Hz sinusoidal control tasks. Closed-loop tracking error is significantly less than open-loop (p < 0.05, Wilcoxon signed rank test, n = 12 comparisons, 4 different cells).

Figure 8. Non-sinusoidal tracking performance

(A) Example implementation (“Cell 5”) on the more naturalistic, non-sinusoidal trajectory. Controller and observer were tuned for a 10 Hz sinusoidally modulated trajectory. The corresponding error spectrum is also shown (bottom). For comparison, the error spectrum of simulated Poisson firing at the reference rate is plotted in light grey. (B) Population tracking error for non-sinusoidal trajectory. 95% confidence intervals for this metric are calculated for simulated Poisson firing at the reference rate and plotted in light grey. Left, simulated LNP performance predicted by design procedure. Middle, experimental closed-loop tracking performance. Right, experimental open-loop tracking performance. (C) Experimental across-trial variability in closed-loop vs. open-loop. Treating 750-ms onward as ‘steady-state’, time-averaged Fano factor calculated in a 250-ms sliding window for the closed- vs. open-loop control cases.