Fundamental principles in bacterial physiology-history, recent progress, and the future with focus on cell size control: a review
- PMID: 29313526
- PMCID: PMC5897229
- DOI: 10.1088/1361-6633/aaa628
Fundamental principles in bacterial physiology-history, recent progress, and the future with focus on cell size control: a review
Abstract
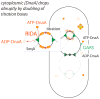
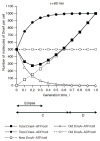
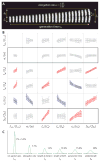
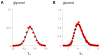
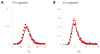
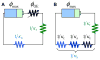
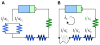
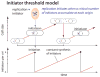
Bacterial physiology is a branch of biology that aims to understand overarching principles of cellular reproduction. Many important issues in bacterial physiology are inherently quantitative, and major contributors to the field have often brought together tools and ways of thinking from multiple disciplines. This article presents a comprehensive overview of major ideas and approaches developed since the early 20th century for anyone who is interested in the fundamental problems in bacterial physiology. This article is divided into two parts. In the first part (sections 1-3), we review the first 'golden era' of bacterial physiology from the 1940s to early 1970s and provide a complete list of major references from that period. In the second part (sections 4-7), we explain how the pioneering work from the first golden era has influenced various rediscoveries of general quantitative principles and significant further development in modern bacterial physiology. Specifically, section 4 presents the history and current progress of the 'adder' principle of cell size homeostasis. Section 5 discusses the implications of coarse-graining the cellular protein composition, and how the coarse-grained proteome 'sectors' re-balance under different growth conditions. Section 6 focuses on physiological invariants, and explains how they are the key to understanding the coordination between growth and the cell cycle underlying cell size control in steady-state growth. Section 7 overviews how the temporal organization of all the internal processes enables balanced growth. In the final section 8, we conclude by discussing the remaining challenges for the future in the field.
Figures



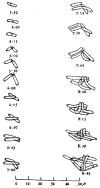


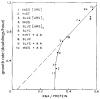


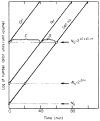
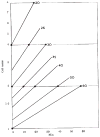
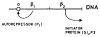







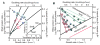


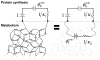


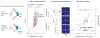

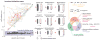

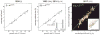


References
-
- Schaechter M, Maal⊘e O, Kjeldgaard NO. Dependency on Medium and Temperature of Cell Size and Chemical Composition during Balanced Growth of Salmonella typhimurium. Journal of General Microbiology. 1958;19:592–606. - PubMed
-
- Kjeldgaard NO, Maal⊘e O, Schaechter M. The Transition Between Different Physiological States During Balanced Growth of Salmonella typhimurium. Journal of General Microbiology. 1958;19:607–616. - PubMed
-
- Cooper S. The origins and meaning of the Schaechter-Maal⊘e-Kjeldgaard experiments. Journal of General Microbiology. 1993;139:1117–1124.
-
- Cooper S. On the fiftieth anniversary of the Schaechter, Maal⊘e, Kjeldgaard experiments: implications for cell-cycle and cell-growth control. BioEssays. 2008;30:1019–1024. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
