Differences in adaptive dynamics determine the success of virus variants that propagate together

Abstract

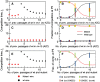
Virus fitness is a complex parameter that results from the interaction of virus-specific characters (e.g. intracellular growth rate, adsorption rate, virion extracellular stability, and tolerance to mutations) with others that depend on the underlying fitness landscape and the internal structure of the whole population. Individual mutants usually have lower fitness values than the complex population from which they come from. When they are propagated and allowed to attain large population sizes for a sufficiently long time, they approach mutation-selection equilibrium with the concomitant fitness gains. The optimization process follows dynamics that vary among viruses, likely due to differences in any of the parameters that determine fitness values. As a consequence, when different mutants spread together, the number of generations experienced by each of them prior to co-propagation may determine its particular fate. In this work we attempt a clarification of the effect of different levels of population diversity in the outcome of competition dynamics. To this end, we analyze the behavior of two mutants of the RNA bacteriophage Qβ that co-propagate with the wild-type virus. When both competitor viruses are clonal, the mutants rapidly outcompete the wild type. However, the outcome in competitions performed with partially optimized virus populations depends on the distance of the competitors to their clonal origin. We also implement a theoretical population dynamics model that describes the evolution of a heterogeneous population of individuals, each characterized by a fitness value, subjected to subsequent cycles of replication and mutation. The experimental results are explained in the framework of our theoretical model under two non-excluding, likely complementary assumptions: (1) The relative advantage of both competitors changes as populations approach mutation-selection equilibrium, as a consequence of differences in their growth rates and (2) one of the competitors is more robust to mutations than the other. The main conclusion is that the nearness of an RNA virus population to mutation-selection equilibrium is a key factor determining the fate of particular mutants arising during replication.

Keywords: computational models; error rate; fitness; population bottlenecks; population dynamics; virus adaptation.

Figure 1.

Code used to indicate the relative amount of wild-type and mutant nucleotides at polymorphic positions. Above, we show example chromatograms for each of the five qualitative intervals of abundance for mutant Qβ_U2776C. The area colored in purple inside the different boxes just below the chromatograms qualitatively represents the relative amount of mutant nucleotides, as used in other figures. Below, vertical, thick blue lines indicate the interval within which the maximum height of the mutant nucleotide band (blue line in the chromatogram) is found relative to that of the wild-type nucleotide (red line in the chromatogram). Numbers in the lower panel are just a loose quantitative approximation to the broad intervals defined, which need to be translated to computational results regarding population fractions: from 0 to 0.1 (first interval, only wild type present), from 0.1 to 0.4 (second, mutant present in a low amount), from 0.4 to 0.6 (third, mutant and wild type present in similar amounts), from 0.6 to 0.9 (fourth, wild type present in a low amount), and from 0.9 to 1 (fifth, only mutant present). Numerical values are only used to guide the eye in comparing experiment and model in Fig. 5.

Figure 2.

Competition experiments between different viral populations. (A) A wild-type biological clone (Qβ_wt, see Section 2.1) was serially transferred in E.coli for ten passages, keeping the moi around 0.1. The clonal virus Qβ_wt (white squares) and the populations obtained after three, five, and ten passages in E.coli (also represented with white squares) were mixed with equal amounts of a biological clone of either the virus Qβ_U2776C (purple squares) or the virus Qβ_U3402C (black squares), and allowed to compete for five passages in E.coli. The consensus sequence of the new populations obtained was determined. The relative amount of each nucleotide, U or C, in the chromatograms is indicated with squares colored with the corresponding amount of white (wild-type nucleotide) and black/purple (mutant nucleotides), see Fig. 1 for definitions. (B) Both the virus Qβ_wt and the mutant Qβ_U2776C were transferred ten times to obtain heterogeneous populations which competed as in (A). (C) As in (A), but with virus Qβ_wt transferred in the presence of 40 µg/ml of AZC. For each experiment, the box in the left-hand side schematically represents the overall organization. Competitions were carried out in duplicate. In all cases the relative amount of the mutant and the wt nucleotide obtained in the two replicas of the same experiment lye in the same interval (Fig. 1) with minor differences that are non-significant in data obtained through Sanger sequencing.

Figure 3.

Competition of the virus Qβ_U2776C with different biological clones isolated from a heterogeneous wild-type population. The population Qβ_wtP10 (Fig. 2A) was used to isolate five biological clones (c1 to c5) which were mixed with equal amounts of the virus Qβ_U2776C. After competition for five passages the consensus sequence of the resulting populations was determined. The relative amount of each nucleotide, U or C, in the chromatograms (estimated as shown in Fig. 1) is indicated with squares colored with the corresponding amount of white (wild-type nucleotide) and purple (mutant nucleotide). Competitions were carried out in duplicate. In all cases the relative amount of the mutant and the wt nucleotide obtained in the two replicas of the same experiment lye in the same interval (Fig. 1) with minor differences that are non-significant in data obtained through Sanger sequencing.

Figure 4.

Dynamics of the populations of wild type and mutant with number of passages. (A, B) Average replicative ability of wild type and mutant for the two different scenarios. The initial distribution of the clonal populations and the asymptotic equilibria for the replicative ability f are plotted in the insets. (A) Scenario 1. Parameters are p_wt = p_mut = 0.2, q_wt = q_mut = 0.01, m_{ef, wt} = m_{ef, mut} = 0.5, F_wt = 10, F_mut = 9, f_{0, wt} = 6, f_{0, mut} = 8. (B) Scenario 2. Parameters are: p_wt = p_mut = 0.5, q_wt = q_mut = 0.001, m_{ef, wt} = 0.5, m_{ef, mut} = 0.25, F_wt = 11, F_mut = 9, f_{0, wt} = f_{0, mut} = 8. (C, D) Single realizations of competitions between the wild-type and the mutant populations for Scenario 1 (C) and Scenario 2 (D). The circles represent populations at each viral generation. In the cases shown in (C) and (D), the mutant displaces the wild-type population after four and eleven passages, respectively.

Figure 5.

Effect of heterogeneity in the competition between the wild type population and the mutant population—Scenario 1. The competition procedure and populations parameters are those of Scenario 1 (Sections 5.1, 5.2, and Fig. 4A). The x-axes denote the number of passages applied to initial populations before starting competition. These previous passages take place in the absence (A, B, m = 1) and presence (C, D, m = 15) of the mutagenic AZC for the wild type, although competitions occur in absence of AZC (m = 1). The competition time and the winner of the competition are plotted in (A, C), while (B, D) show the populations after five passages. (E, F) As above, but now both the wild-type and the mutant competitor are generated upon propagation in the absence of AZC (m = 1). The competition time and the winner of the competition are plotted in (E), while (F) shows the populations after five passages. Experimental results for the wild type competing against clonal virus Qβ_U3402C at 37 °C appear in (B) and (D), and experimental results for the wild type competing against clonal virus Qβ_U2776C at 37 °C are plotted in (B), (D), and (F), as indicated in the legend and using the code defined in Fig. 1.