Mechanically Coupled Reaction-Diffusion Model to Predict Glioma Growth: Methodological Details
- PMID: 29344892
- PMCID: PMC6530463
- DOI: 10.1007/978-1-4939-7493-1_11
Mechanically Coupled Reaction-Diffusion Model to Predict Glioma Growth: Methodological Details
Abstract
Biophysical models designed to predict the growth and response of tumors to treatment have the potential to become a valuable tool for clinicians in care of cancer patients. Specifically, individualized tumor forecasts could be used to predict response or resistance early in the course of treatment, thereby providing an opportunity for treatment selection or adaption. This chapter discusses an experimental and modeling framework in which noninvasive imaging data is used to initialize and parameterize a subject-specific model of tumor growth. This modeling approach is applied to an analysis of murine models of glioma growth.
Keywords: Biophysical stress; Cancer; Diffusion; Finite difference method; Invasion; MRI.
Figures

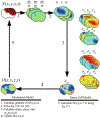

References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

