Infection dynamics on spatial small-world network models

Abstract

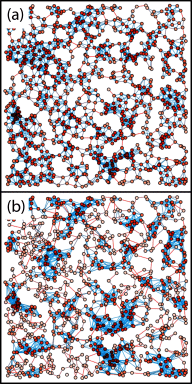
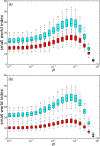
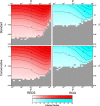
The study of complex networks, and in particular of social networks, has mostly concentrated on relational networks, abstracting the distance between nodes. Spatial networks are, however, extremely relevant in our daily lives, and a large body of research exists to show that the distances between nodes greatly influence the cost and probability of establishing and maintaining a link. A random geometric graph (RGG) is the main type of synthetic network model used to mimic the statistical properties and behavior of many social networks. We propose a model, called REDS, that extends energy-constrained RGGs to account for the synergic effect of sharing the cost of a link with our neighbors, as is observed in real relational networks. We apply both the standard Watts-Strogatz rewiring procedure and another method that conserves the degree distribution of the network. The second technique was developed to eliminate unwanted forms of spatial correlation between the degree of nodes that are affected by rewiring, limiting the effect on other properties such as clustering and assortativity. We analyze both the statistical properties of these two network types and their epidemiological behavior when used as a substrate for a standard susceptible-infected-susceptible compartmental model. We consider and discuss the differences in properties and behavior between RGGs and REDS as rewiring increases and as infection parameters are changed. We report considerable differences both between the network types and, in the case of REDS, between the two rewiring schemes. We conclude that REDS represent, with the application of these rewiring mechanisms, extremely useful and interesting tools in the study of social and epidemiological phenomena in synthetic complex networks.

FIG. 1.

Examples of a RGG (a) and a REDS network (b) of size $N=1000$ and having the same average degree. Red nodes have higher degree while red edges have higher cost and blue edges have lower cost. Note that nodes are distributed according to the same random spatial disposition.

FIG. 2.

The impact of two types of random rewiring, standard (a) and conservative (b), on the small-world index for RGGs (cyan) and REDS networks (red). Each data point represents values for 100 networks.

FIG. 3.

The impact of two types of random rewiring, standard (a) and conservative (b), on critical beta (${\beta }_c$) values for RGGs (cyan) and REDS networks (red). Each data point represents values for 100 networks.

FIG. 4.

Median outbreak size for REDS (left) and RGG networks (right), using either the standard (top) or conservative (bottom) rewiring method. Each point in the graph is subject to a probability, $p$, of rewiring for a range of transmission probabilities, $\beta$: Each cell in these heat maps represents the average size of successful outbreaks, i.e., the median size of the final stable population of infected nodes for 100 outbreaks (one outbreak on each of 100 different networks), ignoring outbreaks that fail. Cells shaded gray represent conditions under which all 100 simulated outbreaks failed.

FIG. 5.

Curves showing the ratio of successful outcomes vs the total number of runs, for each value of the parameter $\beta$, divided by network type (REDS or RGG) and rewiring type (conservative or standard)