Ligand Binding Dynamics for Pre-dimerised G Protein-Coupled Receptor Homodimers: Linear Models and Analytical Solutions
- PMID: 29349610
- PMCID: PMC6722261
- DOI: 10.1007/s11538-017-0387-x
Ligand Binding Dynamics for Pre-dimerised G Protein-Coupled Receptor Homodimers: Linear Models and Analytical Solutions
Abstract
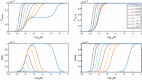
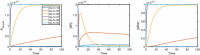
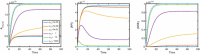
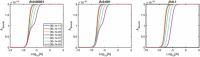
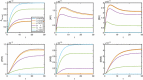
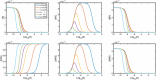
Evidence suggests that many G protein-coupled receptors (GPCRs) are bound together forming dimers. The implications of dimerisation for cellular signalling outcomes, and ultimately drug discovery and therapeutics, remain unclear. Consideration of ligand binding and signalling via receptor dimers is therefore required as an addition to classical receptor theory, which is largely built on assumptions of monomeric receptors. A key factor in developing theoretical models of dimer signalling is cooperativity across the dimer, whereby binding of a ligand to one protomer affects the binding of a ligand to the other protomer. Here, we present and analyse linear models for one-ligand and two-ligand binding dynamics at homodimerised receptors, as an essential building block in the development of dimerised receptor theory. For systems at equilibrium, we compute analytical solutions for total bound labelled ligand and derive conditions on the cooperativity factors under which multiphasic log dose-response curves are expected. This could help explain data extracted from pharmacological experiments that do not fit to the standard Hill curves that are often used in this type of analysis. For the time-dependent problems, we also obtain analytical solutions. For the single-ligand case, the construction of the analytical solution is straightforward; it is bi-exponential in time, sharing a similar structure to the well-known monomeric competition dynamics of Motulsky-Mahan. We suggest that this model is therefore practically usable by the pharmacologist towards developing insights into the potential dynamics and consequences of dimerised receptors.
Keywords: G protein-coupled receptors; Mathematical pharmacology; Ordinary differential equations; Receptor theory.
Figures
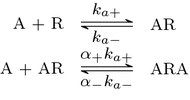

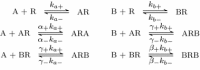








Similar articles
-
Insights into the dynamics of ligand-induced dimerisation via mathematical modelling and analysis.J Theor Biol. 2022 Apr 7;538:110996. doi: 10.1016/j.jtbi.2021.110996. Epub 2022 Jan 24. J Theor Biol. 2022. PMID: 35085533
-
Reinterpreting anomalous competitive binding experiments within G protein-coupled receptor homodimers using a dimer receptor model.Pharmacol Res. 2019 Jan;139:337-347. doi: 10.1016/j.phrs.2018.11.032. Epub 2018 Nov 22. Pharmacol Res. 2019. PMID: 30472462 Free PMC article.
-
Modelling and simulation of biased agonism dynamics at a G protein-coupled receptor.J Theor Biol. 2018 Apr 7;442:44-65. doi: 10.1016/j.jtbi.2018.01.010. Epub 2018 Jan 12. J Theor Biol. 2018. PMID: 29337260 Free PMC article.
-
Old and new ways to calculate the affinity of agonists and antagonists interacting with G-protein-coupled monomeric and dimeric receptors: the receptor-dimer cooperativity index.Pharmacol Ther. 2007 Dec;116(3):343-54. doi: 10.1016/j.pharmthera.2007.05.010. Epub 2007 Jun 14. Pharmacol Ther. 2007. PMID: 17935788 Review.
-
An operational model for GPCR homodimers and its application in the analysis of biased signaling.Drug Discov Today. 2018 Sep;23(9):1591-1595. doi: 10.1016/j.drudis.2018.04.004. Epub 2018 Apr 9. Drug Discov Today. 2018. PMID: 29649573 Review.
Cited by
-
What Can Mathematics Do for Drug Development?Bull Math Biol. 2019 Sep;81(9):3421-3424. doi: 10.1007/s11538-019-00632-x. Bull Math Biol. 2019. PMID: 31332601 Free PMC article. No abstract available.
-
Experimental validation of computerised models of clustering of platelet glycoprotein receptors that signal via tandem SH2 domain proteins.PLoS Comput Biol. 2022 Nov 28;18(11):e1010708. doi: 10.1371/journal.pcbi.1010708. eCollection 2022 Nov. PLoS Comput Biol. 2022. PMID: 36441766 Free PMC article.
-
Classical structural identifiability methodology applied to low-dimensional dynamic systems in receptor theory.J Pharmacokinet Pharmacodyn. 2024 Feb;51(1):39-63. doi: 10.1007/s10928-023-09870-y. Epub 2023 Jun 30. J Pharmacokinet Pharmacodyn. 2024. PMID: 37389744 Free PMC article.
References
-
- Ashyraliyev M, Fomekong-Nanfack Y, Kaandorp JA, Blom JG. Systems biology: parameter estimation for biochemical models. FEBS J. 2009;276(4):886–902. - PubMed
-
- Bai M. Dimerization of g-protein-coupled receptors: roles in signal transduction. Cell Signal. 2004;16(2):175–186. - PubMed
-
- Bridge L. Modeling and simulation of inverse agonism dynamics. Methods Enzymol. 2009;485:559–582. - PubMed
-
- Bridge L, King J, Hill S, Owen M. Mathematical modelling of signalling in a two-ligand g-protein coupled receptor system: agonist-antagonist competition. Math Biosci. 2010;223(2):115–132. - PubMed
-
- Casadó V, Cortés A, Ciruela F, Mallol J, Ferré S, Lluis C, Canela EI, Franco R. Od and new ways to calculate the affinity of agonists and antagonists interacting with g-protein-coupled monomeric and dimeric receptors: The receptor-dimer cooperativity index. Pharmacol Ther. 2007;116(3):343–354. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

