Predictive power of statistical significance

Abstract

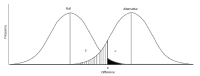
A statistically significant research finding should not be defined as a P-value of 0.05 or less, because this definition does not take into account study power. Statistical significance was originally defined by Fisher RA as a P-value of 0.05 or less. According to Fisher, any finding that is likely to occur by random variation no more than 1 in 20 times is considered significant. Neyman J and Pearson ES subsequently argued that Fisher's definition was incomplete. They proposed that statistical significance could only be determined by analyzing the chance of incorrectly considering a study finding was significant (a Type I error) or incorrectly considering a study finding was insignificant (a Type II error). Their definition of statistical significance is also incomplete because the error rates are considered separately, not together. A better definition of statistical significance is the positive predictive value of a P-value, which is equal to the power divided by the sum of power and the P-value. This definition is more complete and relevant than Fisher's or Neyman-Peason's definitions, because it takes into account both concepts of statistical significance. Using this definition, a statistically significant finding requires a P-value of 0.05 or less when the power is at least 95%, and a P-value of 0.032 or less when the power is 60%. To achieve statistical significance, P-values must be adjusted downward as the study power decreases.

Keywords: Biostatistics; Clinical significance; Positive predictive value; Power; Statistical significance.

Figure 1

According to the classical definition, research findings are considered statistically significant when the difference observed falls in the upper or lower tails of the frequency distribution, represented above in black.

Figure 2

If the observed difference is greater than x, then we consider that the finding is statistically significant and the null hypothesis is rejected. If the difference found is less than x, then we accept the null hypothesis and reject the alternative hypothesis. The area in black represents a Type I error which occurs when the difference is greater than x, but the null hypothesis is in fact true. The lined area represents a Type II error which occurs when the difference found is less than x, but the alternative hypothesis is in fact true.