Quantitative approaches to energy and glucose homeostasis: machine learning and modelling for precision understanding and prediction
- PMID: 29367240
- PMCID: PMC5805973
- DOI: 10.1098/rsif.2017.0736
Quantitative approaches to energy and glucose homeostasis: machine learning and modelling for precision understanding and prediction
Abstract
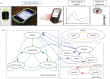
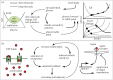
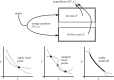
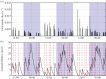
Obesity is a major global public health problem. Understanding how energy homeostasis is regulated, and can become dysregulated, is crucial for developing new treatments for obesity. Detailed recording of individual behaviour and new imaging modalities offer the prospect of medically relevant models of energy homeostasis that are both understandable and individually predictive. The profusion of data from these sources has led to an interest in applying machine learning techniques to gain insight from these large, relatively unstructured datasets. We review both physiological models and machine learning results across a diverse range of applications in energy homeostasis, and highlight how modelling and machine learning can work together to improve predictive ability. We collect quantitative details in a comprehensive mathematical supplement. We also discuss the prospects of forecasting homeostatic behaviour and stress the importance of characterizing stochasticity within and between individuals in order to provide practical, tailored forecasts and guidance to combat the spread of obesity.
Keywords: energy homeostasis; glucostasis; machine learning; mathematical biology.
© 2018 The Authors.
Conflict of interest statement
We declare we have no competing interests.
Figures
Similar articles
-
Mathematical models of energy homeostasis.J R Soc Interface. 2008 Oct 6;5(27):1119-35. doi: 10.1098/rsif.2008.0216. J R Soc Interface. 2008. PMID: 18611843 Free PMC article. Review.
-
Data-driven modeling and prediction of blood glucose dynamics: Machine learning applications in type 1 diabetes.Artif Intell Med. 2019 Jul;98:109-134. doi: 10.1016/j.artmed.2019.07.007. Epub 2019 Jul 26. Artif Intell Med. 2019. PMID: 31383477 Review.
-
Using machine learning approaches for multi-omics data analysis: A review.Biotechnol Adv. 2021 Jul-Aug;49:107739. doi: 10.1016/j.biotechadv.2021.107739. Epub 2021 Mar 29. Biotechnol Adv. 2021. PMID: 33794304 Review.
-
Mathematical modeling of glucose homeostasis and its relationship with energy balance and body fat.Obesity (Silver Spring). 2009 Apr;17(4):632-9. doi: 10.1038/oby.2008.604. Epub 2009 Jan 15. Obesity (Silver Spring). 2009. PMID: 19148129 Review. No abstract available.
-
Emerging role of the brain in the homeostatic regulation of energy and glucose metabolism.Exp Mol Med. 2016 Mar 11;48(3):e216. doi: 10.1038/emm.2016.4. Exp Mol Med. 2016. PMID: 26964832 Free PMC article. Review.
Cited by
-
Development of a Deep Learning Model for Dynamic Forecasting of Blood Glucose Level for Type 2 Diabetes Mellitus: Secondary Analysis of a Randomized Controlled Trial.JMIR Mhealth Uhealth. 2019 Nov 1;7(11):e14452. doi: 10.2196/14452. JMIR Mhealth Uhealth. 2019. PMID: 31682586 Free PMC article. Clinical Trial.
-
In-silico modelling of insulin secretion and pancreatic beta-cell function for clinical applications: is it worth the effort?Front Clin Diabetes Healthc. 2024 Nov 4;5:1452400. doi: 10.3389/fcdhc.2024.1452400. eCollection 2024. Front Clin Diabetes Healthc. 2024. PMID: 39559404 Free PMC article. No abstract available.
-
Dynamical systems approaches to personalized medicine.Curr Opin Biotechnol. 2019 Aug;58:168-174. doi: 10.1016/j.copbio.2019.03.005. Epub 2019 Apr 9. Curr Opin Biotechnol. 2019. PMID: 30978644 Free PMC article. Review.
-
The homeostatic dynamics of feeding behaviour identify novel mechanisms of anorectic agents.PLoS Biol. 2019 Dec 5;17(12):e3000482. doi: 10.1371/journal.pbio.3000482. eCollection 2019 Dec. PLoS Biol. 2019. PMID: 31805040 Free PMC article.
-
Uncovering personalized glucose responses and circadian rhythms from multiple wearable biosensors with Bayesian dynamical modeling.Cell Rep Methods. 2023 Jul 31;3(8):100545. doi: 10.1016/j.crmeth.2023.100545. eCollection 2023 Aug 28. Cell Rep Methods. 2023. PMID: 37671030 Free PMC article.
References
-
- Bishop CM. 2006. Pattern recognition. Mach. Learn. 128, 1–58.
-
- Friedman J, Hastie T, Tibshirani R. 2001. The elements of statistical learning, Vol. 1 Series in statistics Springer Berlin, Germany: Springer.
-
- Murphy KP. 2012. Machine learning: a probabilistic perspective. Cambridge, MA: MIT press.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

