Efficient Sum of Outer Products Dictionary Learning (SOUP-DIL) and Its Application to Inverse Problems

Abstract

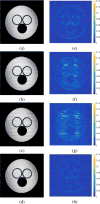
The sparsity of signals in a transform domain or dictionary has been exploited in applications such as compression, denoising and inverse problems. More recently, data-driven adaptation of synthesis dictionaries has shown promise compared to analytical dictionary models. However, dictionary learning problems are typically non-convex and NP-hard, and the usual alternating minimization approaches for these problems are often computationally expensive, with the computations dominated by the NP-hard synthesis sparse coding step. This paper exploits the ideas that drive algorithms such as K-SVD, and investigates in detail efficient methods for aggregate sparsity penalized dictionary learning by first approximating the data with a sum of sparse rank-one matrices (outer products) and then using a block coordinate descent approach to estimate the unknowns. The resulting block coordinate descent algorithms involve efficient closed-form solutions. Furthermore, we consider the problem of dictionary-blind image reconstruction, and propose novel and efficient algorithms for adaptive image reconstruction using block coordinate descent and sum of outer products methodologies. We provide a convergence study of the algorithms for dictionary learning and dictionary-blind image reconstruction. Our numerical experiments show the promising performance and speedups provided by the proposed methods over previous schemes in sparse data representation and compressed sensing-based image reconstruction.

Keywords: Compressed sensing; Convergence analysis; Dictionary learning; Fast algorithms; Inverse problems; Sparsity.

Fig. 1

The SOUP-DILLO Algorithm (due to the ℓ₀ “norm”) for Problem (P1). Superscript t denotes the iterates in the algorithm. The vectors b^t and h^t above are computed efficiently via sparse operations.

Fig. 2

The SOUP-DILLO and SOUP-DILLI image reconstruction algorithms for Problems (P3) and (P4), respectively. Superscript t denotes the iterates. Parameter L can be set very large in practice (e.g., L ∝ ║A^†z║₂).

Fig. 3

Test data (magnitudes of the complex-valued MR data are displayed here). Image (a) is available at http://web.stanford.edu/class/ee369c/data/brain.mat. The images (b)-(e) are publicly available: (b) T2 weighted brain image [69], (c) water phantom [70], (d) cardiac image [71], and (e) T2 weighted brain image [72]. Image (f) is a reference sagittal brain slice provided by Prof. Michael Lustig, UC Berkeley. Image (g) is a complex-valued reference SENSE reconstruction of 32 channel fully-sampled Cartesian axial data from a standard spin-echo sequence. Images (a) and (f) are 512 × 512, while the rest are 256 × 256. The images (b) and (g) have been rotated clockwise by 90° here for display purposes. In the experiments, we use the actual orientations.

Fig. 4

Comparison of dictionary learning approaches for adaptive sparse representation (NSRE and sparsity factors are expressed as percentages): (a) NSRE values for SOUP-DILLO at various λ along with those obtained by performing ℓ₀ block coordinate descent sparse coding (as in (P1)) using learned PADL [41], [55] dictionaries (denoted ‘Post-L0’ in the plot legend); (b) (net) sparsity factors for SOUP-DILLO at various λ along with those obtained by performing ℓ₀ block coordinate descent sparse coding using learned PADL [41], [55] dictionaries; (c) learning times for SOUP-DILLO and PADL; (d) learning times for SOUP-DILLO and OS-DL for various achieved (net) sparsity factors (in learning); (e) NSRE vs. (net) sparsity factors achieved within SOUP-DILLO and OS-DL; and (f) NSRE vs. (net) sparsity factors achieved within SOUP-DILLO along with those obtained by performing ℓ₀ (block coordinate descent) sparse coding using learned OS-DL dictionaries.

Fig. 5

Behavior of SOUP-DILLO MRI (for (P3)) and SOUP-DILLI MRI (for (P4)) for Image (c) with Cartesian sampling and 2.5× undersampling: (a) sampling mask in k-space; (b) magnitude of initial reconstruction y⁰ (PSNR = 24.9 dB); (c) SOUP DILLO MRI (final) reconstruction magnitude (PSNR = 36.8 dB); (d) objective function values for SOUP-DILLO MRI and SOUP-DILLI MRI; (e) reconstruction PSNR over iterations; (f) changes between successive image iterates (║y^t − y^t−1║₂) normalized by the norm of the reference image (║y^ref║₂ = 122.2); (g) normalized changes between successive coefficient iterates (║C^t − C^t−1║_F/║Y^ref║_F) where Y^ref is the patch matrix for the reference image; (h) normalized changes between successive dictionary iterates $({\Vert {\mathbf{D}}^t-{\mathbf{D}}^{t-1}\Vert }_F/\sqrt{J})$ (i) initial real-valued dictionary in the algorithms; and (j) real and (k) imaginary parts of the learnt dictionary for SOUP-DILLO MRI. The dictionary columns or atoms are shown as 6 × 6 patches.

Fig. 6

Results for Image (c) with Cartesian sampling and 2.5× undersampling. The sampling mask is shown in Fig. 5(a). Reconstructions (magnitudes): (a) DLMRI [13]; (b) PANO [75]; (c) ℓ₀ “norm”-based FDLCP [18]; and (d) SOUP-DILLO MRI (with zero-filling initialization). (e)-(h) are the reconstruction error maps for (a)-(d), respectively.