Practical device-independent quantum cryptography via entropy accumulation
- PMID: 29386507
- PMCID: PMC5792631
- DOI: 10.1038/s41467-017-02307-4
Practical device-independent quantum cryptography via entropy accumulation
Abstract
Device-independent cryptography goes beyond conventional quantum cryptography by providing security that holds independently of the quality of the underlying physical devices. Device-independent protocols are based on the quantum phenomena of non-locality and the violation of Bell inequalities. This high level of security could so far only be established under conditions which are not achievable experimentally. Here we present a property of entropy, termed "entropy accumulation", which asserts that the total amount of entropy of a large system is the sum of its parts. We use this property to prove the security of cryptographic protocols, including device-independent quantum key distribution, while achieving essentially optimal parameters. Recent experimental progress, which enabled loophole-free Bell tests, suggests that the achieved parameters are technologically accessible. Our work hence provides the theoretical groundwork for experimental demonstrations of device-independent cryptography.
Conflict of interest statement
The authors declare that they have no competing financial interests.
Figures

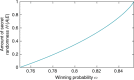
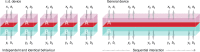


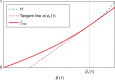

References
-
- Fung CHF, Qi B, Tamaki K, Lo HK. Phase-remapping attack in practical quantum-key-distribution systems. Phys. Rev. A. 2007;75:032314. doi: 10.1103/PhysRevA.75.032314. - DOI
-
- Lydersen L, et al. Hacking commercial quantum cryptography systems by tailored bright illumination. Nat. Photonics. 2010;4:686–689. doi: 10.1038/nphoton.2010.214. - DOI
-
- Weier H, et al. Quantum eavesdropping without interception: an attack exploiting the dead time of single-photon detectors. New J. Phys. 2011;13:073024. doi: 10.1088/1367-2630/13/7/073024. - DOI
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

