High-Dimensional Bayesian Geostatistics
- PMID: 29391920
- PMCID: PMC5790125
- DOI: 10.1214/17-BA1056R
High-Dimensional Bayesian Geostatistics
Abstract
With the growing capabilities of Geographic Information Systems (GIS) and user-friendly software, statisticians today routinely encounter geographically referenced data containing observations from a large number of spatial locations and time points. Over the last decade, hierarchical spatiotemporal process models have become widely deployed statistical tools for researchers to better understand the complex nature of spatial and temporal variability. However, fitting hierarchical spatiotemporal models often involves expensive matrix computations with complexity increasing in cubic order for the number of spatial locations and temporal points. This renders such models unfeasible for large data sets. This article offers a focused review of two methods for constructing well-defined highly scalable spatiotemporal stochastic processes. Both these processes can be used as "priors" for spatiotemporal random fields. The first approach constructs a low-rank process operating on a lower-dimensional subspace. The second approach constructs a Nearest-Neighbor Gaussian Process (NNGP) that ensures sparse precision matrices for its finite realizations. Both processes can be exploited as a scalable prior embedded within a rich hierarchical modeling framework to deliver full Bayesian inference. These approaches can be described as model-based solutions for big spatiotemporal datasets. The models ensure that the algorithmic complexity has ~ n floating point operations (flops), where n the number of spatial locations (per iteration). We compare these methods and provide some insight into their methodological underpinnings.
Keywords: Bayesian statistics; Gaussian process; Nearest Neighbor Gaussian process (NNGP); low rank Gaussian process; predictive process; sparse Gaussian process; spatiotemporal statistics.
Figures


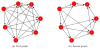

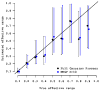
References
-
- Anderson TW. An Introduction to Multivariate Statistical Analysis. 3 New York, NY: Wiley; 2003.
-
- Banerjee S, Carlin BP, Gelfand AE. Hierarchical Modeling and Analysis for Spatial Data. 2 Boca Raton, FL: Chapman & Hall/CRC; 2014.
-
- Banerjee S, Finley AO, Waldmann P, Ericcson T. Hierarchical spatial process models for multiple traits in large genetic trials. Journal of the American Statistical Association. 2010;105:506–521. doi: http://dx.doi.org/10.1198/jasa.2009.ap09068. - DOI - PMC - PubMed
-
- Barry R, Ver Hoef J. Blackbox kriging: Spatial prediction without specifying variogram models. Journal of Agricultural, Biological and Environmental Statistics. 1996;1:297–322.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
