Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2018 Jan 31;3(1):1293-1297.
doi: 10.1021/acsomega.7b01580. Epub 2018 Jan 30.

Asymmetric Choreography in Pairs of Orthogonal Rotors

Antonio Rodríguez-Fortea  1 , Jiří Kaleta  2 , Cécile Mézière  3 , Magali Allain  3 , Enric Canadell  4 , Pawel Wzietek  5 , Josef Michl  2   6 , Patrick Batail  3
Affiliations

Asymmetric Choreography in Pairs of Orthogonal Rotors

Antonio Rodríguez-Fortea et al. ACS Omega. .

Abstract

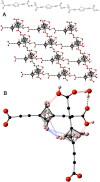
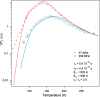
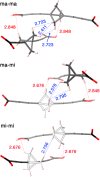
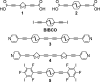
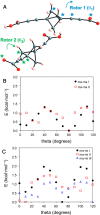
An asymmetric mechanism for correlated motion occurring in noninteracting pairs of adjacent orthogonal 1,4-bis(carboxyethynyl)bicyclo[1.1.1]pentane (BCP) rotators 1 in the solid state is unraveled and shown to play an important role in understanding the dynamics in the crystalline rotor, Bu4N+[1-]·H2O. Single crystal X-ray diffraction and calculation of rotor-rotor interaction energies combined with variable-temperature, variable-field 1H spin-lattice relaxation experiments led to the identification and microscopic rationalization of two distinct relaxation processes.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing financial interest.

Figures

Figure 1
Figure 1
(A) A pair of layers of strings of hydrogen-bonded anions 1 that stack on top of each other along c in Bu4N+[1–]·H2O (Bu4N+ omitted for clarity). Hydrogen-bonded water molecules impose the orthogonal configuration of the two layers within a pair; (B) C–H···H–C (blue dotted lines) and C–H···O (red dotted lines) hydrogen bonds, which determine rotor–rotor and rotor–carboxylate interactions, respectively. Both the majority (0.71) and minority (0.29) occupancy positions (darker and lighter atoms and lines, respectively) of the BCP rotators in dynamic equilibrium in the lattice are represented.
Figure 2
Figure 2
Variable-temperature 1H spin–lattice relaxation time, T1–1, at 57 and 209 MHz for a static crystalline sample of Bu4N+[1–]·H2O. The red and blue solid lines represent the fit of the data to the Kubo–Tomita formula, τc = τ0 exp(Ea/kT), yielding Ea1 = 823 K (1.63 kcal mol–1) and Ea2 = 990 K (1.97 kcal mol–1), respectively, and the attempt correlation times of τ1 = 5.6 × 10–13 s and τ2 = 4.4 × 10–13 s, respectively.
Figure 3
Figure 3
Majority−majority (ma−ma), majority−minority (ma−mi), and minority−minority (mi−mi) configurations given by the crystal structure (Figure 1).
Scheme 1
Scheme 1
Figure 4
Figure 4
(A) Two protocols for the geometry optimization: Either (i) θ1 is given a set value and the geometry of the three blades of each rotor is optimized or (ii) θ1 and θ2 are given set values to impose a motion of both rotors (see text), and the geometry is optimized. The computed energy profiles for the ma–ma (B) and ma–mi (C) pairs of BCP rotators (see the text for a detailed explanation).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

References

    1. Lemouchi C.; Mézière C.; Zorina L.; Simonov S.; Rodríguez-Fortea A.; Canadell E.; Wzietek P.; Auban-Senzier P.; Pasquier C.; Giamarchi T.; Garcia-Garibay M. A.; Batail P. Design and evaluation of a crystalline hybrid of molecular conductors and molecular rotors. J. Am. Chem. Soc. 2012, 134, 7880–7891. 10.1021/ja301484b. - DOI - PubMed
    1. Kaleta J.; Nečas M.; Mazal C. 1,3-Diethynylbicyclo[1.1.1]pentane, a useful molecular building block. Eur. J. Org. Chem. 2012, 4783–4796. 10.1002/ejoc.201200351. - DOI
    2. Kaleta J.; Michl J.; Mazal C. T-shaped molecular building blocks by combined bridgehead and bridge substitution on bicyclo[1.1.1]pentanes. J. Org. Chem. 2010, 75, 2350–2356. 10.1021/jo100169b. - DOI - PubMed
    3. Kaleta J.; Janoušek Z.; Nečas M.; Mazal C. Molecular rods combining o-carborane and bicyclo[1.1.1]pentane cages: an insertion of the triple bond located next to a highly strained cage. Organometallics 2015, 34, 967–972. 10.1021/acs.organomet.5b00002. - DOI
    4. Cipolloni M.; Kaleta J.; Mašát M.; Dron P. I.; Shen Y.; Zhao K.; Rogers C. T.; Shoemaker R. K.; Michl J. Time-resolved fluorescence anisotropy of bicyclo[1.1.1]pentane/tolane-based molecular rods included in tris(o-phenylenedioxy)cyclotriphosphazene (TPP). J. Phys. Chem. C 2015, 119, 8805–8820. 10.1021/acs.jpcc.5b01960. - DOI - PMC - PubMed
    1. Iwamura H.; Mislow K. Stereochemical consequences of dynamic gearing. Acc. Chem. Res. 1988, 21, 175–182. 10.1021/ar00148a007. - DOI
    2. Nakamura M.; Kishimoto K.; Kobori Y.; Abe T.; Yoza K.; Kobayashi K. Self-assembled molecular gear: a 4:1 complex of Rh(III)Cl tetraarylporphyrin and tetra(p-pyridyl)cavitand. J. Am. Chem. Soc. 2016, 138, 12564–12577. 10.1021/jacs.6b07284. - DOI - PubMed
    3. Jiang X.; O’Brien Z. J.; Yang S.; Lai L. H.; Buenaflor J.; Tan C.; Khan S.; Houk K. N.; Garcia-Garibay M. A. Crystal fluidity reflected by fast rotational motion at the core, branches, and Peripheral aromatic groups of a dendrimeric molecular rotor. J. Am. Chem. Soc. 2016, 138, 4650–4656. 10.1021/jacs.6b01398. - DOI - PMC - PubMed
    4. Sanada K.; Ube H.; Shionoya M. Rotational control of a dirhodium-centered supramolecular four-gear system by ligand exchange. J. Am. Chem. Soc. 2016, 138, 2945–2948. 10.1021/jacs.5b13515. - DOI - PubMed
    5. Frantz D. K.; Linden A.; Baldridge K. K.; Siegel J. S. Molecular spur gears comprising triptycene rotators and bibenzimidazole-based stators. J. Am. Chem. Soc. 2012, 134, 1528–1535. 10.1021/ja2063346. - DOI - PubMed
    1. Lemouchi C.; Iliopoulos K.; Zorina L.; Simonov S.; Wzietek P.; Cauchy T.; Rodríguez-Fortea A.; Canadell E.; Kaleta J.; Michl J.; Gindre D.; Chrysos M.; Batail P. Crystalline Arrays of Pairs of Molecular Rotors: Correlated Motion, Rotational Barriers, and Space Inversion-symmetry Breaking due to Conformational Mutations. J. Am. Chem. Soc. 2013, 135, 9366–9376. 10.1021/ja4044517. - DOI - PubMed
    2. Bastien G.; Lemouchi C.; Allain M.; Wzietek P.; Rodríguez-Fortea A.; Canadell E.; Iliopoulos K.; Gindre D.; Chrysos M.; Batail P. Changing gears to neutral in a polymorph of one-dimensional arrays of cogwheel-like pairs of molecular rotor. CrystEngComm 2014, 16, 1241–1244. 10.1039/c3ce42054j. - DOI
    1. Kaleta J.; Michl J.; Mézière C.; Simonov S.; Zorina L.; Wzietek P.; Rodríguez-Fortea A.; Canadell E.; Batail P. Gearing motion in cogwheels pairs of molecular rotors: weak-coupling limit. CrystEngComm 2015, 17, 7829–7834. 10.1039/c5ce01372k. - DOI

LinkOut - more resources