Epidemic spreading in modular time-varying networks

Abstract

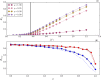
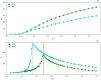
We investigate the effects of modular and temporal connectivity patterns on epidemic spreading. To this end, we introduce and analytically characterise a model of time-varying networks with tunable modularity. Within this framework, we study the epidemic size of Susceptible-Infected-Recovered, SIR, models and the epidemic threshold of Susceptible-Infected-Susceptible, SIS, models. Interestingly, we find that while the presence of tightly connected clusters inhibits SIR processes, it speeds up SIS phenomena. In this case, we observe that modular structures induce a reduction of the threshold with respect to time-varying networks without communities. We confirm the theoretical results by means of extensive numerical simulations both on synthetic graphs as well as on a real modular and temporal network.

Figure 1

Schematic representation of the model. In red, we show active nodes. Straight lines and arcs describe links connecting nodes in the same or in different communities respectively. In the bottom right panel we show the integrated network obtained as the union of G₁, G₂, G₃.

Figure 2

Time evolution of the average total degree, 〈k(a, s, t)〉, for different activity classes and compared with the theoretical function of Eq. 3a,b,c and, evaluated considering a community size equal to the average (i.e. s = 〈s〉). The rescaled time is $t\to \tilde{a}t$ and $\langle k(\tilde{a}t)\rangle$ is plotted. Parameters used are: N = 10⁵, ω = 2.1, ν = 2.1, s_min = 10, μ = 0.9 and T = 10⁵ evolution steps. Each point is an average of 10² simulations.

Figure 3

Plot of the three degree distributions and the theoretical prediction, given in Eq. 4. Parameters used are: N = 10⁵, ω = 2.1, ν = 2.1, s_min = 10, μ = 0.9 and T = 10⁵ evolution steps.

Figure 4

Panel (A) R_∞ as a function of β/γ, for selected values of μ and s_min = 10. Vertical black line represents the theoretical value of the epidemic threshold for μ = 0 as derived in refs^,. Panel (B) R_max, i.e. the max value of R_∞, as a function of μ. In red curves we set s_min = 100, in blue curves s_min = 10. In solid curves, we draw community sizes directly from the community size distribution P(s). In dashed curves, we fix the community sizes as equal to the average value of P(s) for all communities. The 95% confidence interval is in grey. Each point is an average of 10² independent simulations.

Figure 5

Panel (A) Lifetime of the disease L as a function of β/γ, for selected values of μ and when s_min = 10. Vertical lines are the epidemic threshold. Panel (B) Ratio ξ_SIS = β/γ in correspondence of L_max, as a function of μ. In red curves we set s_min = 100, blue curves s_min = 10. Each point is an average of 10² independent simulations. Note that we avoid to simulate μ = 1 because the criterion we follow for the estimation of the threshold does not hold for a network with many connected components.

Figure 6

Panel (A) R_∞ as a function of β/γ for SIR processes diffusing on APS (cyan circles) and on the randomized APS dataset (green circles). Panel (B) L as a function of β/γ for a SIS models evolving on the same two networks. Each point is the average of 10² independent simulations started from 1% of random seeds. We fix γ = 0.05.