The influence of phylodynamic model specifications on parameter estimates of the Zika virus epidemic

Abstract

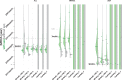
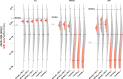
Each new virus introduced into the human population could potentially spread and cause a worldwide epidemic. Thus, early quantification of epidemic spread is crucial. Real-time sequencing followed by Bayesian phylodynamic analysis has proven to be extremely informative in this respect. Bayesian phylodynamic analyses require a model to be chosen and prior distributions on model parameters to be specified. We study here how choices regarding the tree prior influence quantification of epidemic spread in an emerging epidemic by focusing on estimates of the parameters clock rate, tree height, and reproductive number in the currently ongoing Zika virus epidemic in the Americas. While parameter estimates are quite robust to reasonable variations in the model settings when studying the complete data set, it is impossible to obtain unequivocal estimates when reducing the data to local Zika epidemics in Brazil and Florida, USA. Beyond the empirical insights, this study highlights the conceptual differences between the so-called birth-death and coalescent tree priors: while sequence sampling times alone can strongly inform the tree height and reproductive number under a birth-death model, the coalescent tree height prior is typically only slightly influenced by this information. Such conceptual differences together with non-trivial interactions of different priors complicate proper interpretation of empirical results. Overall, our findings indicate that phylodynamic analyses of early viral spread data must be carried out with care as data sets may not necessarily be informative enough yet to provide estimates robust to prior settings. It is necessary to do a robustness check of these data sets by scanning several models and prior distributions. Only if the posterior distributions are robust to reasonable changes of the prior distribution, the parameter estimates can be trusted. Such robustness tests will help making real-time phylodynamic analyses of spreading epidemic more reliable in the future.

Keywords: molecular epidemiology; start of epidemic; substitution rate; tree height; tree prior.

Figure 1.

MCC tree of the 139 ZIKV sequences included in this study. The posterior clade support is displayed at each branching point. The names of all virus sequences that were isolated in Florida, USA, are highlighted in green and all sequences from Brazil are highlighted in magenta. The cluster of sequences highlighted in green represents the twenty-three strains of the USA data set that form one monophyletic cluster upon exclusion of one non-USA sequence. The MCC tree was obtained using the BDSKY model in BEAST 2 with δ = 18.25, three intervals for R_e and a relaxed clock (see Supplementary Figs S1 and S2 for other model parametrizations).

Figure 2.

TempEst estimates of tree heights and clock rates. The tree height and the clock rate (i.e. slope) estimates obtained using TempEst for the three data sets: (A) the complete data set (ALL), (B) the sequences isolated in Brazil (BRAZIL), and (C) the (monophyletic cluster of) sequences isolated in Florida (USA). The tree for each data set was reconstructed using the ML method.

Figure 3.

The effect of addition of sequence data on the tMRCA estimates in the Bayesian analysis. The probability distribution of the estimates of the tMRCA resulting from the analysis with (green) and without (gray) sequences is shown. The figure shows estimates obtained under various model assumptions (labels on the x-axis summarize the models as explained in Table 1) and the three different data sets (header). The median date of MRCA is indicated with a thick solid line and the 95% HPD intervals are marked with thin solid lines. The black dashed, dotted, and dashed-dotted lines represent the tMRCA estimates based on the TempEst analysis (Fig. 2) for the ALL, BRAZIL, and USA data sets, respectively. The gray dashed, dotted, and dashed-dotted lines represent the tMRCA of the LSD estimates for the ALL, BRAZIL, and USA data sets, respectively. The become uninfectious rate in the BD model is set to δ = 18.25, which is the mean estimate in Ferguson et al. (2016). Notice that the median estimates of the tMRCA for the BRAZIL and USA data sets analysed with the Coal model are beyond the limits of the figure, so we state the estimated tree heights below. For the BRAZIL data set, the median tree height estimate of distributions resulting from analyses without sequence data for Coal: 3 × N_e ∼Γ is 1.8 × 10⁶ years, for Coal: 4 × N_e ∼Γ is 1.0 × 10⁶ years and for Coal: 6 × N_e ∼Γ is 3.5 × 10⁵ years. The median tree height estimate of the distribution when sequence data is included for Coal: 3 × N_e ∼Γ is 1026.7 years, for Coal: 4 × N_e ∼Γ is 960.1 years, and for Coal: 6 × N_e ∼Γ is 1039.8 years. For the USA data set, the median tree height estimate of distributions resulting from analyses without sequence data for Coal: 3 × N_e ∼Γ is 2.0 × 10⁶ years, for Coal: 4 × N_e ∼Γ is 1.2 × 10⁶ years, and for Coal: 6 × N_e ∼Γ is 5.3 × 10⁵ years. The median tree height estimate of the distribution when sequence data is included for Coal: 3 × N_e ∼Γ is 460.8 years, for Coal: 4 × N_e ∼Γ is 449.1 years, and for Coal: 6 × N_e ∼Γ is 443.5 years.

Figure 4.

The effect of addition of sequence data on the clock rate estimates in the Bayesian analysis. The probability distribution of the clock rate (rate.mean parameter) estimates resulting from the analysis with (red) and without (gray) sequences is shown. The figure shows estimates obtained under various model assumptions (labels on the x-axis summarize the models as explained in Table 1) and the three different data sets (header). The median clock rate is indicated with a thick solid line and the 95% HPD interval marked with thin solid lines. The black dashed, dotted, and dashed-dotted lines represent the clock rate estimates based on the TempEst analysis (Fig. 2) for the ALL, BRAZIL, and USA data sets, respectively. The gray dashed, dotted, and dashed-dotted lines represent the clock rate of the LSD estimates for the ALL, BRAZIL, and USA data sets, respectively. The become uninfectious rate in the BD model is set to δ = 18.25, which is the mean estimate in Ferguson et al. (2016). The clock rate displayed is in units of s/s/y, i.e. subst/site/year.

Figure 5.

Birth–death skyline plot based on the USA data set. We used the BDSKY model allowing six intervals for R_e and 1 mean value for the sampling probability. Opaque coloring for the effective reproductive number, R_e (orange), and the sampling probability (cyan), depict the results of analyses without sequence data, the darker shades display estimates after the addition of sequence data. The vertical dashed magenta lines and crosses indicate the sampling time points of the viral sequences. The magenta curve summarizes the lineages-through-time plot averaged over all MCMC samples without the burn-in (first 10% of samples). For all parameters we show the 95% confidence intervals and the median estimates (solid central line).