Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2018 Feb 6;18(1):19.
doi: 10.1186/s12874-018-0479-9.

Using an onset-anchored Bayesian hierarchical model to improve predictions for amyotrophic lateral sclerosis disease progression

Alex G Karanevich  1 , Jeffrey M Statland  2 , Byron J Gajewski  3 , Jianghua He  3
Affiliations

Using an onset-anchored Bayesian hierarchical model to improve predictions for amyotrophic lateral sclerosis disease progression

Alex G Karanevich et al. BMC Med Res Methodol. .

Abstract

Background: Amyotrophic Lateral Sclerosis (ALS), also known as Lou Gehrig's disease, is a rare disease with extreme between-subject variability, especially with respect to rate of disease progression. This makes modelling a subject's disease progression, which is measured by the ALS Functional Rating Scale (ALSFRS), very difficult. Consider the problem of predicting a subject's ALSFRS score at 9 or 12 months after a given time-point.

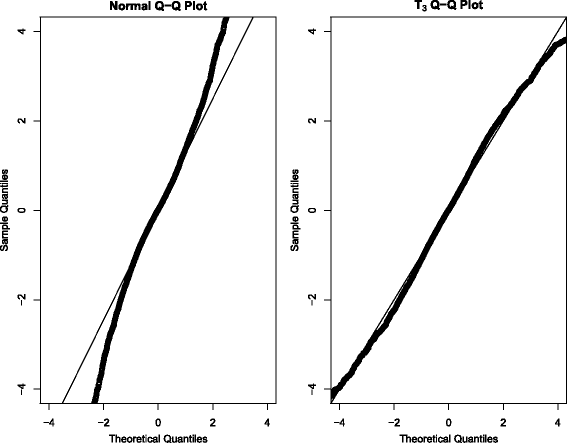
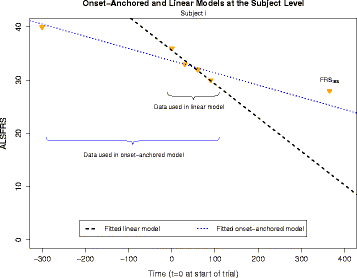
Methods: We obtained ALS subject data from the Pooled Resource Open-Access ALS Clinical Trials Database, a collection of data from various ALS clinical trials. Due to the typical linearity of the ALSFRS, we consider several Bayesian hierarchical linear models. These include a mixture model (to account for the two potential classes of "fast" and "slow" ALS progressors) as well as an onset-anchored model, in which an additional artificial data-point, using time of disease onset, is utilized to improve predictive performance.

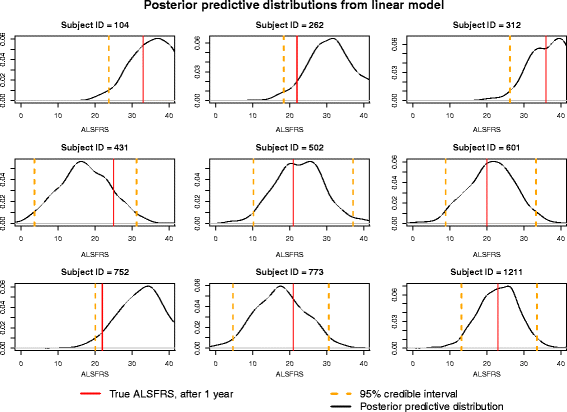
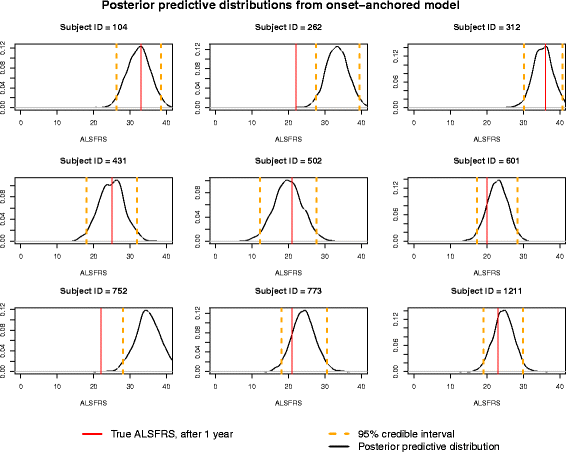
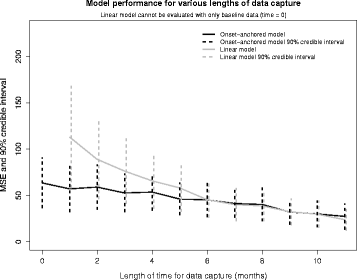
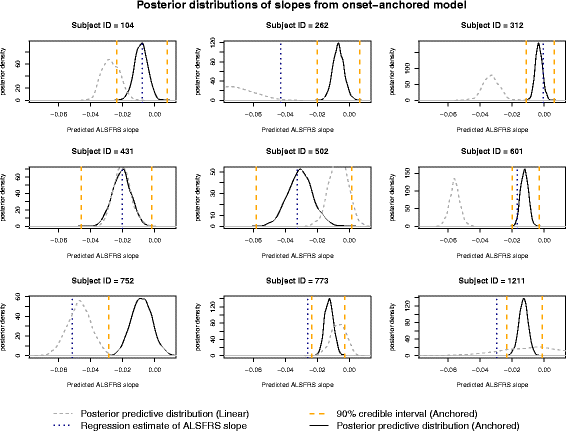
Results: The onset-anchored model had a drastically reduced posterior predictive mean-square-error distributions, when compared to the Bayesian hierarchical linear model or the mixture model under a cross-validation approach. No covariates, other than time of disease onset, consistently improved predictive performance in either the Bayesian hierarchical linear model or the onset-anchored model.

Conclusions: Augmenting patient data with an additional artificial data-point, or onset anchor, can drastically improve predictive modelling in ALS by reducing the variability of estimated parameters at the cost of a slight increase in bias. This onset-anchored model is extremely useful if predictions are desired directly after a single baseline measure (such as at the first day of a clinical trial), a feat that would be very difficult without the onset-anchor. This approach could be useful in modelling other diseases that have bounded progression scales (e.g. Parkinson's disease, Huntington's disease, or inclusion-body myositis). It is our hope that this model can be used by clinicians and statisticians to improve the efficacy of clinical trials and aid in finding treatments for ALS.

Keywords: ALS; ALSFRS; Hierarchical modelling; Onset-anchor; Prediction; Pro-act.

PubMed Disclaimer

Conflict of interest statement

Ethics approval and consent to participate

In all of the trials that generated the data included in this database, study protocols were approved by the participating medical centers and all participating patients gave informed consent. De-identified data from these trials were donated to the PRO-ACT database for research purposes only and under the explicit conditions that Prize4Life and all users of the data would maintain the anonymity of subjects and not attempt to discover the identity of any subject. In the rare cases where donated data was not already completely anonymized, donated data was further anonymized following the HIPAA de-identification conventions for personal health information: any potential patient initials and/or dates of birth were removed, new randomized subject numbers were created, and wherever possible, trial-specific information was removed in the merging of datasets, including trial center identity and location, trial dates, or other identifying information. This project was deemed not to constitute human subjects research and the need for ethical approval for this work was waived by the University of Kansas Medical Center’s Human Research Protection Program.

Consent for publication

Not applicable

Competing interests

Jeffrey M. Statland is a consultant for aTyr, Acceleron, Fulcrum, Regeneron, and Strongbridge. The remaining authors declare that they have no competing interests.

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Figures

Fig. 1
Fig. 1
QQ plots for the residuals obtained from fitting simple linear regression models on subjects that had at least 5 ALSFRS measurements
Fig. 2
Fig. 2
Ordinary least-squares estimates for two models: the linear model uses data from zero to 3 months only, while the onset-anchored model includes an additional artificial data-point. This time point is given as (x, y)= (time-point of disease onset-time, maximal ALSFRS of 40)
Fig. 3
Fig. 3
Comparison of posterior MSE distribution for four types of hierarchical models: linear, onset-anchored, mixture, and mixture with the additional data-point used in the onset-anchored model. This is from a single replicate of the cross-validation analysis, but this separation of distributions is typical
Fig. 4
Fig. 4
Posterior predictive distributions for a random sample of subjects’ FRS365 obtained through cross-validation utilizing the standard linear model
Fig. 5
Fig. 5
Posterior predictive distributions for a random sample of subjects’ FRS365 obtained through cross-validation utilizing the onset-anchored model
Fig. 6
Fig. 6
The effect of changing the number of months of data used for prediction in both the linear and onset-anchored models. This effect is measured by the MSE (and associated 90% credible interval) resulting from a single replicate of the cross-validation analysis for both models. As the length of data-capture increases the benefits from including an anchor decreases
Fig. 7
Fig. 7
Posterior predictive distributions for a random sample of subjects’ ALSFRS slope obtained through cross-validation utilizing the onset-anchored model. The regression estimate of the ALSFRS slope (vertical dotted line) was calculated using ordinary least squares on subject’s full data
See this image and copyright information in PMC

References

    1. Armon C, Graves MC, Moses D, Forte DK, Sepulveda L, Darby SM, et al. Linear estimates of disease progression predict survival in patients with amyotrophic lateral sclerosis. Muscle Nerve. 2000;23(6):874–882. doi: 10.1002/(SICI)1097-4598(200006)23:6<874::AID-MUS5>3.0.CO;2-U. - DOI - PubMed
    1. Magnus T, Beck M, Giess R, Puls I, Naumann M, Toyka KV. Disease progression in amyotrophic lateral sclerosis: predictors of survival. Muscle Nerve. 2002;25(5):709–714. doi: 10.1002/mus.10090. - DOI - PubMed
    1. Gordon PH, Cheng B, Salachas F, Pradat PF, Bruneteau G, Corcia P, et al. Progression in ALS is not linear but is curvilinear. J Neurol. 2010;257(10):1713–1717. doi: 10.1007/s00415-010-5609-1. - DOI - PubMed
    1. Ikeda K, Hirayama T, Takazawa T, Kawabe K, Iwasaki Y. Relationships between disease progression and serum levels of lipid, urate, creatinine and ferritin in Japanese patients with amyotrophic lateral sclerosis: a cross-sectional study. Intern Med. 2012;51(12):1501–1508. doi: 10.2169/internalmedicine.51.7465. - DOI - PubMed
    1. Kimura F, Fujimura C, Ishida S, Nakajima H, Furutama D, Uehara H, et al. Progression rate of ALSFRS-R at time of diagnosis predicts survival time in ALS. Neurology. 2006;66(2):265–267. doi: 10.1212/01.wnl.0000194316.91908.8a. - DOI - PubMed

Publication types