full-FORCE: A target-based method for training recurrent networks
- PMID: 29415041
- PMCID: PMC5802861
- DOI: 10.1371/journal.pone.0191527
full-FORCE: A target-based method for training recurrent networks
Abstract
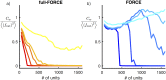
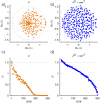
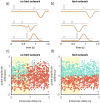
Trained recurrent networks are powerful tools for modeling dynamic neural computations. We present a target-based method for modifying the full connectivity matrix of a recurrent network to train it to perform tasks involving temporally complex input/output transformations. The method introduces a second network during training to provide suitable "target" dynamics useful for performing the task. Because it exploits the full recurrent connectivity, the method produces networks that perform tasks with fewer neurons and greater noise robustness than traditional least-squares (FORCE) approaches. In addition, we show how introducing additional input signals into the target-generating network, which act as task hints, greatly extends the range of tasks that can be learned and provides control over the complexity and nature of the dynamics of the trained, task-performing network.
Conflict of interest statement
Figures
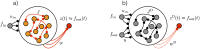




References
-
- LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521: 436–444. doi: 10.1038/nature14539 - DOI - PubMed
-
- Sussillo D. Neural circuits as computational dynamical systems. Curr. Opin. Neurobiol. 2014;25: 156–163. doi: 10.1016/j.conb.2014.01.008 - DOI - PubMed
-
- Werbos PJ. Generalization of backpropagation with application to a recurrent gas market model. Neural Networks. 1988;1: 339–356. doi: 10.1016/0893-6080(88)90007-X - DOI
-
- Abbott LF, DePasquale B, Memmesheimer R-M. Building functional networks of spiking model neurons. Nature Neurosci. 2016;19: 350–355. doi: 10.1038/nn.4241 - DOI - PMC - PubMed
-
- Haykin S. Adaptive Filter Theory. Upper Saddle River, NJ: Prentice Hall; 2002.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

