Hydrodynamics in Cell Studies

Abstract

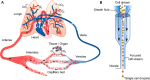
Hydrodynamic phenomena are ubiquitous in living organisms and can be used to manipulate cells or emulate physiological microenvironments experienced in vivo. Hydrodynamic effects influence multiple cellular properties and processes, including cell morphology, intracellular processes, cell-cell signaling cascades and reaction kinetics, and play an important role at the single-cell, multicellular, and organ level. Selected hydrodynamic effects can also be leveraged to control mechanical stresses, analyte transport, as well as local temperature within cellular microenvironments. With a better understanding of fluid mechanics at the micrometer-length scale and the advent of microfluidic technologies, a new generation of experimental tools that provide control over cellular microenvironments and emulate physiological conditions with exquisite accuracy is now emerging. Accordingly, we believe that it is timely to assess the concepts underlying hydrodynamic control of cellular microenvironments and their applications and provide some perspective on the future of such tools in in vitro cell-culture models. Generally, we describe the interplay between living cells, hydrodynamic stressors, and fluid flow-induced effects imposed on the cells. This interplay results in a broad range of chemical, biological, and physical phenomena in and around cells. More specifically, we describe and formulate the underlying physics of hydrodynamic phenomena affecting both adhered and suspended cells. Moreover, we provide an overview of representative studies that leverage hydrodynamic effects in the context of single-cell studies within microfluidic systems.

Figure 1

Contrasting blood circulation inside the body with artificially created structures used to realize hydrodynamic focusing in single-cell analysis. (A) The heart pumps oxygen-rich blood from its left chamber into the circulatory system. Blood flows through arteries and arterioles before it reaches capillaries supplying target organs and cells with nutrients and oxygen. Subsequently, oxygen-poor blood continues through venules and veins back into the right chamber of the heart. From there, it is pumped to the lungs, where red blood cells are replenished with oxygen. The blood finally flows back into the left heart chamber, from where it can re-enter the circulatory system. (B) Hydrodynamic focusing in flow cytometry. A sheath fluid flow within a capillary engulfs a central cell-laden stream. Control of the velocities and/or densities of the two liquid streams allows formation of a stable two-layer flow, with cells moving in single file toward a detector and outlet nozzle.

Figure 2

Graphical summary. This article contains three main sections: hydrodynamics in adherent and nonadherent cell studies and in cell studies on open surfaces and substrates. Each section begins with hydrodynamic theory and design rules and then discusses key parameters that engender novel applications. (Top left) Adapted with permission from ref (28). Copyright 2013 the Royal Society of Chemistry. (Top right) Adapted with permission from ref (29). Copyright 2011 the American Institute of Physics. Adapted with permission from ref (30). Copyright 2015 the American Institute of Physics. Adapted with permission from ref (31). Copyright 2010 the American Institute of Physics. (Bottom left) Adapted with permission from ref (32). Copyright 2005 MacMillan Publishers. Adapted with permission from ref (33). Copyright 2014 MacMillan Publishers. Adapted from ref (34). Copyright 2010 the American Chemical Society. (Bottom right) Adapted with permission from ref (35). Copyright 2014 the Royal Society of Chemistry. Adapted from ref (36). Copyright 2014 the American Chemical Society.

Figure 3

Hydrodynamic effects on adhered cells. (A) Channel flow and entrance length in a microfluidic channel. (B) Schematic velocity profiles for a rectangular and a circular cross-section microchannel. (C) Velocity profile for a rectangular cross-section channel with w = 250 μm, h = 50 μm, and Q = 10 μL min^–1. (D and E) Associated wall shear rate distributions. (F) Shear rate per unit flow rate plotted for various channel heights and aspect ratios. (G) A multishear cell culture device with channels of various sizes and independent inlets and outlets. (H) A multishear device with channels of various hydraulic resistance and cell culture chambers of equal dimension all connected to a common inlet and outlet. The varying flow rate in each culture chamber will result in a different level of shear experienced by the wall-adhered cells. (I) Periodic and variable shear-culture channels for exposing a population of cells to variable levels of shear.

Figure 4

Global cell adhesion studies in shear flow. (A) REF52 cells were exposed to a stepwise shear gradient, with the adhesion strength being analyzed at a shear stress of 22 dyn cm^–2 (2.2 Pa). (i) Cells are able to adapt to the shear stress at longer exposure times (>9 min), with the cell adhesion strength being higher than at shorter exposure times. At low exposure times, cell adhesion is not affected by shear. (B) A tapered channel microfluidic device for comprehensive cell adhesion analysis allows the measurement of detachment kinetics and shear-induced motion. The detachment efficiencies of MDA-MB-231 and D. discoideum (i) were calculated from the detachment kinetics measured (ii). The critical shear level at which 50% of the cells are detached was assessed for four data sets: D. discoideum on a glass substrate in highly conditioned medium (green ▼) and in fresh medium (blue, ▲) and in fresh medium on APTES-coated substrate (red +), as well as MDA-MB-231 on a collagen-coated substrate (black, ●). (C) Biomechanics of cell rolling: shear flow, cell surface adhesion, and cell deformability were examined by monitoring cells via an installed mirror (i). The cell substrate contact length, L_c, as well as the cell height, H_c, were measured for different shear levels (ii) using finite element analysis. (D) Substrate-dependent adhesion of cells in channels having different hydrodynamic resistances (i). At high shear, appropriate fibronectin coating leads to enhanced cell adhesion (ii). At a shear of 2000 dyn cm^–2 (200 Pa) applied for 12 min, only 10% of the cells detached, but at twice that shear stress, more than 90% of the cells came off the surface in the same time period (iii). (A) Adapted with permission from ref (77). Copyright 2010 the Royal Society of Chemistry. (B) Adapted with permission from ref (78). Copyright 2012 the American Institute of Physics. (C) Adapted with permission from ref (79). Copyright 2000 Elsevier. (D) Adapted from ref (80). Copyright 2004 the American Chemical Society.

Figure 5

Using hydrodynamics to modulate the shear stress on cells. (A) Flow stimulation of bone cells with steady flow resulting in a wall shear stress of 2 N m^–2, oscillating flow (−2 to 2 N m^–2) and pulsatile flow (0 to 2 N m^–2). Dynamic flows were applied with sinusoidal profiles of 0.5, 1.0, and 2.0 Hz. The stimulation of cells with pulsatile and steady flow (Pls, S) was significantly stronger than with oscillating (Osc) flow. (B) Multishear device containing ten channels of varying lengths (top). HUVECs were immunostained for intracellular and extracellular vWF factor (red), rhodamine phalloidon (green), and Hoechst (blue) after 20 h of perfusion under different shear flows. For shear stresses above 5 dyn cm^–2 (0.5 Pa), cells exhibited significantly higher vWF secretion and were at least 30% smaller in size. (Scale bar: 50 μm). (C) A multishear microfluidic device for quantitative analysis of calcium dynamics in osteoblasts. (i) Four different shear levels (0.3, 0.6, 1.2, and 3 dyn cm^–2) were exerted on osteoblasts to study the cytosolic calcium concentration Ca2+ dynamics. (ii and iii) The cytosolic calcium concentration increased with shear stress from 0.3 to 3 dyn cm^–2 (0.03 to 0.30 Pa); the response to shear was delayed with an activation threshold between 0.3 and 0.6 dyn cm^–2 (0.03 and 0.06 Pa). (D) Effect of flow rate and shear level on the shape and orientation of endothelial cells in a straight microfluidic channel. At high flow rates (large pump, high shear) and flow exposure times, the HDMECs tend to align and elongate significantly (decreasing Supporting Information) in the direction of flow (decreased angle of alignment). In contrast, at low flow rates (small pump, low shear), the flow and flow exposure time do not affect the cell shape and orientation. (A) Adapted with permission from ref (83). Copyright 1998 Elsevier. (B) Adapted with permission from ref (85). Copyright 2009 the Royal Society of Chemistry. (C) Adapted with permission from ref (87). Copyright 2011 Elsevier. (D) Adapted from ref (88). Copyright 2005 the American Chemical Society.

Figure 6

Shearotaxis and artificial interstitial fluid flows. (A) Dependence of migration directionality on the reversal of the flow direction in a straight channel. At low frequencies, (a) the cells migrate steadily along the streamline. At high reversing frequency (b), the cells are trapped. (B) A pressure gradient between P₁ and P₀ establishes an artificial interstitial flow microenvironment for studying (e.g., cancer cell progression). (C) Fibroblasts in the center of the device were subjected to a minimal osmosis driven flow mimicking the interstitial fluid. (D) Motility of D. discoideum depends on mechanical and chemical stimuli. Shear induced migration along the streamlines. Calcium concentration affected the speed but had no influence on the directionality of cell migration. (A) Adapted with permission from ref (74). Copyright 2014 Public Library of Science. (B) Adapted with permission from ref (72). Copyright 2011 National Academy of Sciences. (C) Adapted with permission from ref (103). Copyright 2009 Royal Society of Chemistry. (D) Adapted with permission from ref (92). Copyright 2005 Company of Biologists Ltd. (E) Adapted with permission from ref (73). Copyright 2003 Company of Biologists Ltd.

Figure 7

Hydrodynamic effects on cell differentiation. (A) Microfluidic device to present mechanical stimuli to cells. Mechanical stimuli are modulated by changing the pressure on the membrane. At selected times (1, 3, and 7 days), cells were assessed by monitoring ALP, a differentiation marker. The stimulated groups with 5 and 20 kPa stimulus at day 3 compared with the control group. (B) Shear-stress stimulation on a multiplexed microfluidic device for rat bone-marrow stromal cell differentiation enhancement. Chambers with different flow resistances enable a multiplexed analysis. Cells were exposed to shear forces of 0.0009, 0.022, and 0.33 dyn cm^–2 for 10 min in different chambers. The cell differentiation ratio was visualized by immunohistochemistry for the differentiation markers. Increased flow shear leads to an enhancement of the differentiation ratio. (C) Osteoblast-based continuous perfusion microfluidic system for drug screening. Cells were cultured either in a microchannel under hydrodynamic shear or cultured on a static well plate for a period of 10 days. In the microchannel culture, the shear stress of 0.07 dyn cm^–2 (7 × 10^–3 Pa) induced enhanced GFP compared with the static culture, suggesting that shear induces differentiation. ALP, an enzyme marker of osteoblasts, supported the results of GFP expression. (A) Adapted with permission from ref (104). Copyright 2007 Royal Society of Chemistry. (B) Adapted with permission from ref (105). Copyright 2015 MDPI AG. (C) Adapted with permission from ref (106). Copyright 2008 Springer.

Figure 8

Spatiotemporal concentration profiles of autocrine and paracrine factors and their effect on the cell phenotype. (A) LIF activates STAT3 and induces self-renewal. In this study, the effects of the flow rate, the position of the flow field and the local field organization on STAT3 activation and the fate of mESC were analyzed, mathematically described, and compared with the static culture. (B and C) Effect of endogenous autocrine and paracrine factors on stem cell differentiation of mESC. (B) In a flow chamber, Nanog, Klf4, and Rex1 were washed off from stem cells, which induces differentiation. (C) Adding endogenous factors to the medium (complex medium, CM) allows the impact of each of these factors on stem cell self-renewal and maintenance of the undifferentiated stage to be studied. (D) Stable TNFα gradient across a rectangular diffusion chamber. Across the chamber, there is a minimal flow that does not disturb the spatiotemporal gradients of secreted molecules from the cells. Sink and drain channels perpendicular to the chamber maintain the gradient constant, which allows global effects of TNFα on cells to be studied without disrupting the local cell–cell pattern. (A and B) Adapted with permission from refs ( and 110). Copyright 2012 Proceedings of the National Academy of Sciences. (C) Adapted with permission from ref (111). Copyright 2011 Public Library of Science. (D) Adapted with permission from ref (112). Copyright 2013 Royal Society of Chemistry.

Figure 9

Mechanical microenvironments. (A) Durotaxis of fibroblasts on a microelastic polyacrylamide gradient gel. Manipulation of the elasticity jumps affects cell migration speed and mechanotaxis efficiency. (B) Characteristic alignment of C2C12 cells on a grooved microfluidic channel substrate. Depending on the orientation of the flow and the geometry of the grooved substrate, cultured cells orient into characteristic 3D cellular constructs. Aligned C2C12 3D cellular constructs showed enhanced differentiation into skeletal muscles than randomly aligned cells. (C) Micropillar arrays allow for the monitoring of cell contraction forces as well as for the investigation of the force directionality of cells grown on the micropillar substrates. (D) Application of a vacuum allows for the mimicking of the breathing motions in the lung. Modulated strain on the artificial alveolus affects cancer cell proliferation and migration. (A) Adapted with permission from ref (124). Copyright 2008 Elsevier. (B) Adapted with permission from ref (28). Copyright 2013 Royal Society of Chemistry. (C) Adapted from ref (131). Copyright 2012 Royal Society of Chemistry.

Figure 10

Various hydrodynamic forces acting on suspended cells in a flow. (A) Drag forces are exerted on a particle in the direction of the flow or in the opposite direction of the flow, depending on the direction of the relative velocity. Drag forces are present in both the creeping and the inertial flow regime. (B) Magnus forces on a rotating particle as a result of a rotation-induced pressure imbalance. Magnus forces are always directed toward the side having the higher relative velocity. (C and D) Wall forces for a particle or a cell moving parallel or perpendicular to a wall. The fluid between the particle and the wall has a lower velocity and higher pressure, forcing the particle away from the wall. (E) Saffman forces for a particle in a simple shear flow. The Saffman force is always directed toward the side having the higher relative velocity and as a result will have a different direction depending on the relative velocity of the particle. (F) Shear-induced lift force as a result of the parabolic velocity profile and the varying relative velocity on either side of the particle. This force is directed toward the side having the higher relative velocity. In a microchannel with a parabolic velocity distribution, a particle will be pushed toward the channel walls.

Figure 11

Hydrodynamic effects on suspended cells in flow. (A) Cells in parabolic flow will be driven away from the center and the wall and find an equilibrium position at 0.3 H away from the center. (B) In simple shear flow, the only effect is the wall effect that drives the cells away from the wall until they find a stable position at the center. (C) Hydrodynamic forces acting on a particle in parabolic (dashed) and simple shear (solid) flow profiles. (D) Stable equilibrium positions for particles in an inertial Poiseuille flow in channels with different cross sections. (E and F) Effect of increasing Re on the stable positions for cells in channels with different cross sections. (G) Effect of the particle size on the inertial lift experienced by the particle. The larger the particle, the bigger the inertial lift forces, and as a result, the particle will find an equilibrium position closer to the walls. (H) Effect of varying the aspect ratio in the stable positions in a rectangular channel. (I) Curved microchannels result in cross-sectional, secondary flows around the bend, which affect the focusing of particles according to their size. (J) Secondary Dean flows occur as a result of mismatching fluid inertia along the curved channel and the resulting migration of the cells due to the interplay between the secondary flow drag force and the inertial lift forces. Two potential equilibrium positions in the vicinity of the inner and outer wall of the curve have been reported in the literature, with the inner wall position being the most frequently reported stable position for particles in curved channels. (K) Steps, converging-diverging channels, and wall irregularities will result in secondary Dean flow recirculation and, similarly to curved channels, induce a size-dependent separation of particles in the channel. (C) Reproduced with permission from ref (160). Copyright 1974 Cambridge University Press.

Figure 12

Hydrodynamic effects for selective cell sorting. (A) Hydrodynamic-lift effects are induced by a viscous orthogonally flowing sheath fluid. Height of RBCs (z position in the channel) significantly increases, whereas platelets flow along the wall. (B) Expansion-contraction channels for separating rare cancer cells from blood cells. The combination of inertial lift and viscous drag forces acts on particles of various sizes. The contraction channel aligns the center of inertia of the rare cells (green) toward the channel center, while the other cells are still flowing along the channel walls. (C) Dual role of Dean forces for focusing larger particles (7.32 μm) in a single equilibrium position and transposing smaller (1.9 μm) particles from the inner half to the outer half of the microchannel cross section. (D) Dean flow and centrifugal forces induced by the serpentine channel design induce size-based differential equilibrium positions of the particles. Larger cells migrate toward the center, whereas smaller particles flow along the wall. (E) Obstacles translate cells based on their deformability and viscosity. In the channel, the cells experience a hydrodynamic force and an elastic force as they are being deformed by the ridges. The difference in the gradient of the free energy of soft and stiff cells leads to different transverse forces. These forces deflect the cell trajectories in the microchannel perpendicularly to the ridge, depending on cell stiffness. This method enabled the separation of K562 and Jurkat cells. (F) Randomly distributed particles experience an elastic force, proportional to the particle volume. Large particles migrate toward the centerline. Larger particles laterally migrate farther than smaller particles while flowing in the second stage. (G) Deterministic lateral displacement: particles that are smaller than the lane width follow the streamlines in lane 1, pass through lane 3 in the second row, then pass lane 2 in the third row, flow through lane 1, whereas particles with a radius larger than the width will be displaced repeatedly. (A) Adapted with permission from ref (168). Copyright 2012 the American Institute of Physics. (B) Adapted with permission from ref (169). Copyright 2011 Royal Society of Chemistry. (C) Adapted with permission from ref (165). Copyright 2008 Royal Society of Chemistry. (D) Adapted with permission from ref (172). Copyright 2015 Nature Publishing Group. (E) Adapted with permission from ref (173). Copyright 2013 Wang et al. (F) Adapted with permission from ref (174). Copyright 2015 the American Institute of Physics. (G) Adapted with permission from ref (175). Copyright 2004 the American Association for Advancement of Science.

Figure 13

Physical and purely hydrodynamic trapping in microchannels. (A) Cells of a first type (green) are first trapped on the frontside of the traps. Then a backflow guides the cells into the single traps on the back-side of the double trap. Then cells of a second type (red) are flowed into the channel, and single cells of cell both types are trapped in the front two-cell trap. (B) Individual cells are transported into the trap sites, where they act as plugs. This increases the flow resistance of path 1 dramatically. Under this condition, the cell medium prefers to travel in the main channel (bypassing mode), the cell travels around the filled trap site, and is captured in the next empty trap site. (C) The resistance in the main channel is higher than the resistance across the 3 μm high gap, and thus the cells are trapped in the empty cavity. (D) The array of circular holes traps and funnels the cells into the cavities aligned below the holes. (E) In the high aspect ratio inlet channels, the wall lift force is the main force and aligns the particles near the channel wall. In the channel expansions, the shear gradient lift force lifts the larger particles, which are trapped by microvortices. (F) Hydrodynamic forces act on the particles in the flow field, and manipulation of the stagnation point along the extensional axis can be used to steer the particle. (A) Adapted with permission from refs ( and 187). Copyright 2015 and 2009 Macmillan Publishers, respectively. (B) Adapted with permission from ref (30). Copyright 2015 American Institute of Physics. (C) Adapted with permission from ref (185). Copyright 2010 Royal Society of Chemistry. (D) Adapted with permission from ref (186). Copyright 2015 Royal Society of Chemistry. (E) Adapted with permission from ref (29). Copyright 2011 American Institute of Physics. (F) Adapted with permission from ref (31). Copyright 2010 American Institute of Physics.

Figure 14

Asymmetric geometries leverage hydrodynamic focusing properties in microchannels. (A) The sheath fluid is exposed to the Dean flow at the contraction region and wraps the RBC suspension close to side 2 (s2). RBCs simultaneously begin to shift toward side 1 (s1). This leads to a three-dimensional focusing of the RBCs in a cross-sectional plane of the microchannel. (B) Asymmetric elements induce secondary flows and facilitate particle focusing with Newtonian and non-Newtonian fluids. (C) The sheath flow maintains the cells near the inner wall of the curved channel, and the Dean flow shifts the cells toward the opposite wall. (D) Particles undergo two opposing forces, the elastic force (F_E) and the Dean drag force (F_D). The Dean elasto-inertial focusing (DEF) band is created on the right-hand side of the confined spiral channel (red box). In the region of the DEF band, lateral migration is dictated by the competition of F_D and F_E. Single-line particle focusing has been achieved when using a viscoelastic medium but not in a Newtonian medium. (E) Three-dimensional hydrodynamic flow focusing of dye, particles, and cells in a microfluidic device by using two bends of opposite curvature. (A) Adapted with permission from ref (189). Copyright 2009 the Royal Society of Chemistry. (B) Adapted with permission from ref (190). Copyright 2015 the American Institute of Physics. (C) Adapted with permission from ref (191). Copyright 2016 Springer. (D) Adapted with permission from ref (192). Copyright 2013 Nature Publishing Group. (E) Adapted with permission from ref (146). Copyright 2007 Proceedings of the National Academy of Sciences.

Figure 15

Cell deformation in microchannels and blood cell studies. (A) Hydrodynamic cell stretching of MCF-7 cells. MCF-7 cells are delivered to a T-junction at high flow rates, where they are exposed to and deformed by the shear strain. Also, the deformability of native populations of leukocytes and malignant cells in pleural effusions was investigated and the disease state in patients with cancer and immune activation predicted with a sensitivity of 91% and a specificity of 86%. (B) Analysis of the shape recovery of Plasmodium falciparum-infected and healthy RBCs. Elastic RBCs cells of 8 μm diameter as well as infected cells in the early ring stages flowed through the cavities of 8, 6, 4, and 2 μm width. Trophozoite stages traversed 6 and 8 μm but failed to transverse 2 μm and partly also 4 μm. Schizont stages traversed only 8 μm. Uninfected RBCs easily passed through the 2 μm constriction. (C) Microfluidic biomechanical assay for RBCs parasitized by Plasmodium falciparum. Individual RBCs are deformed by flowing them through multiple funnel-shaped constrictions with openings ranging from 5 down to 1 μm. Parasitized cells from the ring through the Schizont stage were shown to be 1.5 to 200 times stiffer than uninfected cells. (D) The role of actin organization and myosin-II activity during the different stages of leukocyte trafficking through narrow capillaries using specific drugs (Lat-A, Jpk, and Blb). The channel was 20 μm wide, with constrictions of 4 μm. Case I: control and Jpk- and Lat-A-treated cells have a puck shape, with a diameter of 17 μm and height of W = 4 μm. Case II: Blb-treated cells have a roughly parallelepiped shape, with dimensions of 4, 16, and 29 μm. (A) Adapted with permission from ref (195). Copyright 2012 National Academy of Sciences. (B) Adapted with permission from ref (204). Copyright 2003 National Academy of Sciences. (C) Adapted with permission from ref (203). Copyright 2012 Royal Society of Chemistry. (D) Adapted with permission from ref (205). Copyright 2009 Elsevier.

Figure 16

Shear effects on receptor–ligand binding kinetics. (A) Studies of the kinetics of bond formation and dissociation of activated neutrophils and endothelial cells on the surface on a flow chamber. A minimal shear drag force was exerted that was lower than the strength of a single molecular bond. The graph shows the observed relation of the probability of neutrophile adhesion to the bilayer and the flow velocity. x Axis: (flow velocity)⁻¹, y axis: probability of adhesion. (B) In a flow chamber, binding and unbinding events of neutrophils flowing over a bilayer containing P-selectin tethers were monitored to understand the biophysics of cell rolling. The k_off values shown in the graph were calculated by comparing the binding rates in shear stressed and nonstressed systems. x Axis: shear stress vs off-rate; y axis: k_off (s^–1). (C) Comparison of the abilities of the two models to account for the data. Predictions (curves) of model II (a and b) and model I (c and d) for the unsaturated (a and c) and saturated (b and d) bindings. (D) Dependence of k_off on the shear stress for WT and mutant substrates. On the basis of Goldman’s equations, the force acting on a platelet in shear flow was calculated. (A) Adapted with permission from ref (207). Copyright 1993 Elsevier. (B) Adapted with permission from ref (208). Copyright 1995 MacMillan Publisher (C) Adapted with permission from ref (209). Copyright 1998 Elsevier. (D) Adapted with permission from ref (210). Copyright 2002 Elsevier.

Figure 17

Hydrodynamic effects on adhered and suspended cells in open flows. (A) Open flow over adhered cells and corresponding momentum and mass transfer boundary layers. (B) Stagnation flow above a substrate covered with adhered cells and the corresponding boundary layer formation. (C) A suspended cell flowing over a flat surface in open flow and corresponding hydrodynamic forces on the cell. (D) A suspended cell in stagnation flow over a flat surface and corresponding hydrodynamic force on the cell.

Figure 18

Hydrodynamic manipulation of cells on immersed surfaces. (A) The fluidFM aspirates cells to the tip (negative pressure). A positive pressure pulse allows the cell to be placed at a selected location. (B) Trypsin is hydrodynamically confined to a selected adherent cell until the cell detaches. After detachment, the cell is aspirated into the MFP head. (C) Single cell analysis is leveraged by detaching a cell using hydrodynamic confinement of trypsin. The detached cell is then lysed and analyzed on-chip. (D) Hydrodynamics are leveraged to guide axons using a micropipette. (E) Single cell drug testing is performed by confining pharmacological agents on a selected cell. (F) The single-cell pipet is used to retrieve multiple cells from a suspension culture and trap a single cell from the aspirated cells. The method allows reinjection of the single cell. (A) Adapted with permission from ref (35). Copyright 2014 the Royal Society of Chemistry. (B) Adapted with permission from ref (32). Copyright 2005 MacMillan Publishers. (C) Adapted with permission from ref (33). Copyright 2014 MacMillan Publishers. (D) Adapted with permission from ref (216). Copyright 2015 Nature Publishing Group. (E) Adapted from ref (34). Copyright 2010 the American Chemical Society. (F) Adapted from ref (36). Copyright 2014 the American Chemical Society.