Maximizing the information learned from finite data selects a simple model
- PMID: 29434042
- PMCID: PMC5828598
- DOI: 10.1073/pnas.1715306115
Maximizing the information learned from finite data selects a simple model
Abstract
We use the language of uninformative Bayesian prior choice to study the selection of appropriately simple effective models. We advocate for the prior which maximizes the mutual information between parameters and predictions, learning as much as possible from limited data. When many parameters are poorly constrained by the available data, we find that this prior puts weight only on boundaries of the parameter space. Thus, it selects a lower-dimensional effective theory in a principled way, ignoring irrelevant parameter directions. In the limit where there are sufficient data to tightly constrain any number of parameters, this reduces to the Jeffreys prior. However, we argue that this limit is pathological when applied to the hyperribbon parameter manifolds generic in science, because it leads to dramatic dependence on effects invisible to experiment.
Keywords: Bayesian prior choice; effective theory; information theory; model selection; renormalization group.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
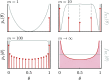

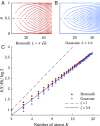
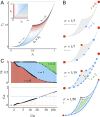

References
-
- Kadanoff LP. Scaling laws for Ising models near . Physics. 1966;2:263–272.
-
- Wilson KG. Renormalization group and critical phenomena. 1. Renormalization group and the Kadanoff scaling picture. Phys Rev. 1971;B4:3174–3183.
-
- Cardy JL. Scaling and Renormalization in Statistical Physics. Cambridge Univ Press; Cambridge, UK: 1996.
-
- Waterfall JJ, et al. Sloppy-model universality class and the Vandermonde matrix. Phys Rev Lett. 2006;97:150601–150604. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

