Holographic Traction Force Microscopy
- PMID: 29445207
- PMCID: PMC5813032
- DOI: 10.1038/s41598-018-21206-2
Holographic Traction Force Microscopy
Abstract
Traction Force Microscopy (TFM) computes the forces exerted at the surface of an elastic material by measuring induced deformations in volume. It is used to determine the pattern of the adhesion forces exerted by cells or by cellular assemblies grown onto a soft deformable substrate. Typically, colloidal particles are dispersed in the substrate and their displacement is monitored by fluorescent microscopy. As with any other fluorescent techniques, the accuracy in measuring a particule's position is ultimately limited by the number of evaluated fluorescent photons. Here, we present a TFM technique based on the detection of probe particle displacements by holographic tracking microscopy. We show that nanometer scale resolutions of the particle displacements can be obtained and determine the maximum volume fraction of markers in the substrate. We demonstrate the feasibility of the technique experimentally and measure the three-dimensional force fields exerted by colorectal cancer cells cultivated onto a polyacrylamide gel substrate.
Conflict of interest statement
The authors declare no competing interests.
Figures
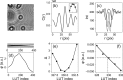

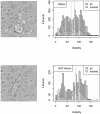
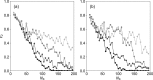
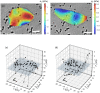

References
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

