Minimum energy control for complex networks
- PMID: 29453421
- PMCID: PMC5816648
- DOI: 10.1038/s41598-018-21398-7
Minimum energy control for complex networks
Abstract
The aim of this paper is to shed light on the problem of controlling a complex network with minimal control energy. We show first that the control energy depends on the time constant of the modes of the network, and that the closer the eigenvalues are to the imaginary axis of the complex plane, the less energy is required for complete controllability. In the limit case of networks having all purely imaginary eigenvalues (e.g. networks of coupled harmonic oscillators), several constructive algorithms for minimum control energy driver node selection are developed. A general heuristic principle valid for any directed network is also proposed: the overall cost of controlling a network is reduced when the controls are concentrated on the nodes with highest ratio of weighted outdegree vs indegree.
Conflict of interest statement
The authors declare no competing interests.
Figures



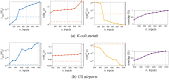
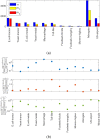
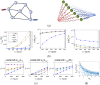

References
-
- Commault C, Dion J-M, van der Woude JW. Characterization of generic properties of linear structured systems for efficient computations. Kybernetika. 2002;38:503–520.
-
- Liu, Y.-Y. & Barabási, A.-L. Control Principles of Complex Networks. ArXiv e-prints (2015).
-
- Nepusz, T. & Vicsek, T. Controlling edge dynamics in complex networks. Nature Physics (2012).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

