Functional brain connectivity is predictable from anatomic network's Laplacian eigen-structure
- PMID: 29454104
- PMCID: PMC6170160
- DOI: 10.1016/j.neuroimage.2018.02.016
Functional brain connectivity is predictable from anatomic network's Laplacian eigen-structure
Abstract
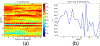
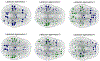
How structural connectivity (SC) gives rise to functional connectivity (FC) is not fully understood. Here we mathematically derive a simple relationship between SC measured from diffusion tensor imaging, and FC from resting state fMRI. We establish that SC and FC are related via (structural) Laplacian spectra, whereby FC and SC share eigenvectors and their eigenvalues are exponentially related. This gives, for the first time, a simple and analytical relationship between the graph spectra of structural and functional networks. Laplacian eigenvectors are shown to be good predictors of functional eigenvectors and networks based on independent component analysis of functional time series. A small number of Laplacian eigenmodes are shown to be sufficient to reconstruct FC matrices, serving as basis functions. This approach is fast, and requires no time-consuming simulations. It was tested on two empirical SC/FC datasets, and was found to significantly outperform generative model simulations of coupled neural masses.
Keywords: Eigen decomposition; Functional network; Graph theory; Laplacian; Networks; Structural network.
Copyright © 2018. Published by Elsevier Inc.
Figures
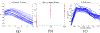

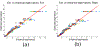




References
-
- Albright TD, 1984. Direction and orientation selectivity of neurons in visual area MT of the macaque. J Neurophysiol. 52 (6), 1106–1130. - PubMed
-
- Aleman-Gomez Y, Melie-García L, Valdes-Hernandez P, June 2006. IBASPM: toolbox for automatic parcellation of brain structures. Hum. Brain Mapp
-
- Ashburner J, 2007. A fast diffeomorphic image registration algorithm. NeuroImage 38 (1), 95–113. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

