Modeling the hematocrit distribution in microcirculatory networks: A quantitative evaluation of a phase separation model
- PMID: 29457313
- PMCID: PMC6024080
- DOI: 10.1111/micc.12445
Modeling the hematocrit distribution in microcirculatory networks: A quantitative evaluation of a phase separation model
Abstract
Objective: Theoretical models are essential tools for studying microcirculatory function. Recently, the validity of a well-established phase separation model was questioned and it was claimed that it produces problematically low hematocrit predictions and lack of red cells in small diameter vessels. We conducted a quantitative evaluation of this phase separation model to establish common ground for future research.
Methods: Model predictions were validated against a comprehensive database with measurements from 4 mesenteric networks. A Bayesian data analysis framework was used to integrate measurements and network model simulations into a combined analysis and to model uncertainties related to network boundary conditions as well as phase separation model parameters. The model evaluation was conducted within a cross-validation scheme.
Results: Unlike the recently reported results, our analysis demonstrated good correspondence in global characteristics between measurements and predictions. In particular, predicted hematocrits for vessels with small diameters were consistent with measurements. Incorporating phase separation model parameter uncertainties further reduced the hematocrit validation error by 17% and led to the absence of red-cell-free segments. Corresponding model parameters are presented as alternatives to standard parameters.
Conclusions: Consistent with earlier studies, our quantitative model evaluation supports the continued use of the established phase separation model.
Keywords: Bayesian inference; flow simulation; microcirculatory measurements; phase separation effect; quantitative model evaluation.
© 2018 John Wiley & Sons Ltd.
Figures
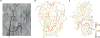


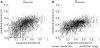







Similar articles
-
Blood flow in microvascular networks. Experiments and simulation.Circ Res. 1990 Oct;67(4):826-34. doi: 10.1161/01.res.67.4.826. Circ Res. 1990. PMID: 2208609
-
Model-based inference from microvascular measurements: Combining experimental measurements and model predictions using a Bayesian probabilistic approach.Microcirculation. 2017 May;24(4):10.1111/micc.12343. doi: 10.1111/micc.12343. Microcirculation. 2017. PMID: 27987383 Free PMC article.
-
Redistribution of red blood cell flow in microcirculatory networks by hemodilution.Circ Res. 1992 Jun;70(6):1113-21. doi: 10.1161/01.res.70.6.1113. Circ Res. 1992. PMID: 1576733
-
Rheology of the microcirculation.Clin Hemorheol Microcirc. 2003;29(3-4):143-8. Clin Hemorheol Microcirc. 2003. PMID: 14724335 Review.
-
The cell-free layer in microvascular blood flow.Biorheology. 2009;46(3):181-9. doi: 10.3233/BIR-2009-0530. Biorheology. 2009. PMID: 19581726 Review.
Cited by
-
Modeling Reactive Hyperemia to Better Understand and Assess Microvascular Function: A Review of Techniques.Ann Biomed Eng. 2023 Mar;51(3):479-492. doi: 10.1007/s10439-022-03134-5. Epub 2023 Jan 28. Ann Biomed Eng. 2023. PMID: 36709231 Free PMC article. Review.
-
The role of leptomeningeal collaterals in redistributing blood flow during stroke.PLoS Comput Biol. 2023 Oct 23;19(10):e1011496. doi: 10.1371/journal.pcbi.1011496. eCollection 2023 Oct. PLoS Comput Biol. 2023. PMID: 37871109 Free PMC article.
-
Predicting Vessel Diameter Changes to Up-Regulate Biphasic Blood Flow During Activation in Realistic Microvascular Networks.Front Physiol. 2020 Oct 16;11:566303. doi: 10.3389/fphys.2020.566303. eCollection 2020. Front Physiol. 2020. PMID: 33178036 Free PMC article.
-
In vitro investigations of red blood cell phase separation in a complex microchannel network.Biomicrofluidics. 2020 Jan 2;14(1):014101. doi: 10.1063/1.5127840. eCollection 2020 Jan. Biomicrofluidics. 2020. PMID: 31933711 Free PMC article.
-
Brief disruptions in capillary flow result in rapid onset of hypoxia.Neurophotonics. 2025 Jun;12(Suppl 2):S22803. doi: 10.1117/1.NPh.12.S2.S22803. Epub 2025 Aug 12. Neurophotonics. 2025. PMID: 40800118 Free PMC article.
References
-
- Corrigendum. Microcirculation. 2015;22:434–434. - PubMed
-
- Bennett ND, Croke BFW, Guariso G, Guillaume JHA, Hamilton SH, Jakeman AJ, Marsili-Libelli S, Newham LTH, Norton JP, Perrin C, Pierce SA, Robson B, Seppelt R, Voinov AA, Fath BD, Andreassian V. Characterising performance of environmental models. Environmental Modelling & Software. 2013;40:1–20.
-
- Box GEP, Tiao GC. Bayesian inference in statistical analysis. Reading, Mass: Addison-Wesley Pub. Co; 1973.
-
- Cleveland WS, Loader C. Smoothing by Local Regression: Principles and Methods. In: Härdle W, Schimek MG, editors. Statistical Theory and Computational Aspects of Smoothing: Proceedings of the COMPSTAT ’94 Satellite Meeting held in Semmering, Austria, 27–28 August 1994. Heidelberg: Physica-Verlag HD; 1996. pp. 10–49.
-
- Cokelet GR, Pries AR, Kiani MF. Observations on the Accuracy of Photometric Techniques Used to Measure Some In Vivo Microvascular Blood Flow Parameters. Microcirculation. 1998;5:61–70. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

