Towards an analytic solution for pulsed CEST

Abstract

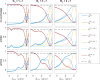
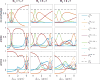
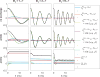
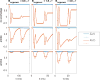
Chemical exchange saturation transfer (CEST) is an imaging method based on magnetization exchange between solutes and water. This exchange generates changes in the measured signal after off-resonance radiofrequency irradiation. Although the analytic solution for CEST with continuous wave (CW) irradiation has been determined, most studies are performed using pulsed irradiation. In this work, we derive an analytic solution for the CEST signal after pulsed irradiation that includes both short-time rotation effects and long-time saturation effects in a two-pool system corresponding to water and a low-concentration exchanging solute pool. Several approximations are made to balance the accuracy and simplicity of the resulting analytic form, which is tested against numerical solutions of the coupled Bloch equations and is found to be largely accurate for amides at high fields, but less accurate at the higher exchange rates, lower offsets and typically higher irradiation powers of amines.

Keywords: CERT; CEST; analytic; exchange.

FIGURE A1

${\mathrm{Z}}_{\mathrm{a}}^{\text{ss},\text{pul}}$ analytic results (dots, Equations 1, 2 and 4–12) versus experimental measures (lines) in a creatine phantom as a function of the B₁-induced rotation angle when irradiating at the solute resonance (Δω_b = 0). Pulsed irradiation is applied with α between 150 and 420°, t_p = 16.8 ms and a root-mean-square B₁ amplitude of 0.6 µT

FIGURE 1

(a) A chemical exchange saturation transfer (CEST) Z-spectrum is the steady-state normalized water z-magnetization $(Z_{\mathrm{a}}^{\text{ss}})$ after radiofrequency irradiation at a frequency offset Δω_a from the water resonant frequency ω_a. (b) The radiofrequency irradiation pulse train consists of a series of shaped (typically Gaussian) pulses (blue line), which are approximated in this work by a train of square pulses (red line). The train is repeated until reaching a steady state, which may take hundreds of pulses. The transverse magnetization is spoiled between pulses

FIGURE 2

$Z_{\mathrm{a}}^{\text{ss},\text{ pul}}$ analytic (dots, Equations 1–3 and 5–12) versus numerical (lines) results as a function of irradiation offset (which changes Δω_a and Δω_b). Note the strong agreement, especially near the solute resonances at 3.5 ppm (amide) and 2.0 ppm (amine). Discrepancies occur at higher B₁ values, faster exchange rates and small Δω_a values. As in all the figures, the plot rows correspond to no exchange (k_b = 0.0001 s⁻¹, Δω_b−Δω_a = 3.5 ppm), amide exchange (k_b = 50 s⁻¹, Δω_b−Δω_a = 3.5 ppm) and amine exchange (k_b = 1000 s⁻¹, Δω_b−Δω_a = 2.0 ppm). The plot columns correspond to differing roots of the mean square B₁ amplitudes. (In the continuous wave plots below, the columns correspond to simple differing B₁ amplitudes)

FIGURE 3

$Z_{\mathrm{a}}^{\text{ss},\text{ pul}}$ analytic (dots, Equations 1, 2 and 4–12) versus numerical (lines) results as a function of the B₁-induced rotation angle when irradiating at the solute resonance (Δω_b = 0). Note the strong agreement for amides. This is the key result: that the analytic form accurately models the effect of solute rotation on the steady-state water magnetization, at least at the larger offsets and slower exchange rates of amides

FIGURE 4

Short-time evolution of Z_a(t) and Z_b(t), together with the projection of $Z_{\mathrm{a}}^{\mathrm{i}}$ along the a-pool effective field. Note that the time scale of Z_b(t) variations is large relative to that of Z_a(t) oscillations (at rate ω_eff,a) and short relative to that of Z_a(t) exponential decay (at rate R_1ρ). Hence, for purposes of deriving the Z_b(t) evolution, Z_a(t) can be approximated by the projection of $Z_{\mathrm{a}}^{\mathrm{i}}$. This approximation fails for amines at large irradiation powers, where Z_b(t) oscillates quickly and Z_a(t) has non-trivial exponential decay

FIGURE 5

Analytic (dots) versus numerically determined (lines) eigenvalues of the 6 × 6 evolution matrix in Equation 14. Note the strong agreement

FIGURE 6

Analytic (Equations 15 and 16, dots) and numerical (lines) values of the a-pool component amplitudes as a function of the irradiation frequency offset. Note the reasonable agreement, as long as there is limited direct water (a-pool) rotation, which has been ignored in our analytic form. We have also ignored R_1ρ,fast and ω_eff,b contributions to the a-pool, all of which give negligible contributions

FIGURE 7

Analytic (Equations 17 and 23–27, dots) and numerical (lines) values of the b-pool component amplitudes as a function of the irradiation frequency. Note the reasonable agreement, as long as direct water (a-pool) rotation effects are limited by avoiding small offsets and high powers. We have ignored ω_eff,a contributions to the b-pool, which appear to give small contributions, except for fast amine exchange near Δω_a = 0

FIGURE 8

Analytic (dots) versus numerical (lines) Z_a(t) terms versus time, when irradiating at the solute resonance. Note the general agreement, which decreases for fast and small offset amine exchange and for high B₁ = 6 µT irradiation amplitude

FIGURE 9

Analytic (dots) versus numerical (lines) Z_b(t) terms versus time, when irradiating at the solute resonance. Note the very strong agreement, except for amine exchange at the highest (6 µT) irradiation amplitude

FIGURE 10

Analytic (dots) and numerical (lines) Z_a(t) and Z_b(t) values during two Gaussian pulses applied at the solute resonance. An α = 3π rotation is applied in order to clearly illustrate the ability of the analytic solution to accurately model solute rotations. However, note the deviations, especially at fast amine exchange rates