A network model of behavioural performance in a rule learning task
- PMID: 29483357
- PMCID: PMC5832697
- DOI: 10.1098/rstb.2017.0275
A network model of behavioural performance in a rule learning task
Abstract
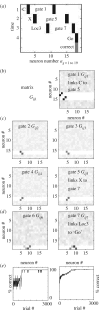
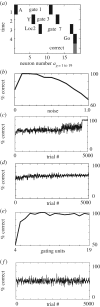
Humans demonstrate differences in performance on cognitive rule learning tasks which could involve differences in properties of neural circuits. An example model is presented to show how gating of the spread of neural activity could underlie rule learning and the generalization of rules to previously unseen stimuli. This model uses the activity of gating units to regulate the pattern of connectivity between neurons responding to sensory input and subsequent gating units or output units. This model allows analysis of network parameters that could contribute to differences in cognitive rule learning. These network parameters include differences in the parameters of synaptic modification and presynaptic inhibition of synaptic transmission that could be regulated by neuromodulatory influences on neural circuits. Neuromodulatory receptors play an important role in cognitive function, as demonstrated by the fact that drugs that block cholinergic muscarinic receptors can cause cognitive impairments. In discussions of the links between neuromodulatory systems and biologically based traits, the issue of mechanisms through which these linkages are realized is often missing. This model demonstrates potential roles of neural circuit parameters regulated by acetylcholine in learning context-dependent rules, and demonstrates the potential contribution of variation in neural circuit properties and neuromodulatory function to individual differences in cognitive function.This article is part of the theme issue 'Diverse perspectives on diversity: multi-disciplinary approaches to taxonomies of individual differences'.
Keywords: acetylcholine; muscarinic receptors; neocortex; rule learning.
© 2018 The Author(s).
Conflict of interest statement
The authors have no conflicts of interest.
Figures


Similar articles
-
Supervised Learning in Spiking Neural Networks for Precise Temporal Encoding.PLoS One. 2016 Aug 17;11(8):e0161335. doi: 10.1371/journal.pone.0161335. eCollection 2016. PLoS One. 2016. PMID: 27532262 Free PMC article.
-
Biologically plausible learning in recurrent neural networks reproduces neural dynamics observed during cognitive tasks.Elife. 2017 Feb 23;6:e20899. doi: 10.7554/eLife.20899. Elife. 2017. PMID: 28230528 Free PMC article.
-
Learning rule of homeostatic synaptic scaling: presynaptic dependent or not.Neural Comput. 2011 Dec;23(12):3145-61. doi: 10.1162/NECO_a_00210. Epub 2011 Sep 15. Neural Comput. 2011. PMID: 21919784
-
Reward-dependent learning in neuronal networks for planning and decision making.Prog Brain Res. 2000;126:217-29. doi: 10.1016/S0079-6123(00)26016-0. Prog Brain Res. 2000. PMID: 11105649 Review.
-
Synaptic computation and sensory processing in neocortical layer 2/3.Neuron. 2013 Apr 10;78(1):28-48. doi: 10.1016/j.neuron.2013.03.020. Neuron. 2013. PMID: 23583106 Review.
Cited by
-
A neural circuit model for a contextual association task inspired by recommender systems.Hippocampus. 2020 Apr;30(4):384-395. doi: 10.1002/hipo.23194. Epub 2020 Feb 14. Hippocampus. 2020. PMID: 32057161 Free PMC article.
-
Temporal Flexibility of Systems Consolidation and the Synaptic Occupancy/Reset Theory (SORT): Cues About the Nature of the Engram.Front Synaptic Neurosci. 2019 Feb 13;11:1. doi: 10.3389/fnsyn.2019.00001. eCollection 2019. Front Synaptic Neurosci. 2019. PMID: 30814946 Free PMC article.
-
A Cellular Mechanism Underlying Enhanced Capability for Complex Olfactory Discrimination Learning.eNeuro. 2019 Feb 12;6(1):ENEURO.0198-18.2019. doi: 10.1523/ENEURO.0198-18.2019. eCollection 2019 Jan-Feb. eNeuro. 2019. PMID: 30783614 Free PMC article.
-
Taxonomies of psychological individual differences: biological perspectives on millennia-long challenges.Philos Trans R Soc Lond B Biol Sci. 2018 Apr 19;373(1744):20170152. doi: 10.1098/rstb.2017.0152. Philos Trans R Soc Lond B Biol Sci. 2018. PMID: 29483338 Free PMC article.
-
Prefrontal oscillations modulate the propagation of neuronal activity required for working memory.Neurobiol Learn Mem. 2020 Sep;173:107228. doi: 10.1016/j.nlm.2020.107228. Epub 2020 Jun 17. Neurobiol Learn Mem. 2020. PMID: 32561459 Free PMC article.
References
-
- Chang AE, Ren Y, Whiteman AS, Stern CE.. 2017. Evaluating the relationship between activity in frontostriatal regions and successful and unsuccessful performance of a context-dependent rule learning task. Program no. 619.19, Society for Neuroscience Meeting Planner. San Diego, CA: Society for Neuroscience. Online.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

