A comparative analysis of surface and bulk contributions to second-harmonic generation in centrosymmetric nanoparticles

Abstract

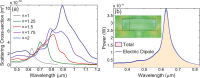
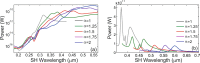
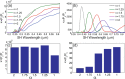
Second-harmonic generation (SHG) from nanoparticles made of centrosymmetric materials provides an effective tool to characterize many important properties of photonic structures at the subwavelength scale. Here we study the relative contribution of surface and bulk effects to SHG for plasmonic and dielectric nanostructures made of centrosymmetric materials in both dispersive and non-dispersive regimes. Our calculations of the far-fields generated by the nonlinear surface and bulk currents reveal that the size of the nanoparticle strongly influences the amount and relative contributions of the surface and bulk SHG effects. Importantly, our study reveals that, whereas for plasmonic nanoparticles the surface contribution is always dominant, the bulk and surface SHG effects can become comparable for dielectric nanoparticles, and thus they both should be taken into account when analyzing nonlinear optical properties of all-dielectric nanostructures.

Figure 1

Schematics of the analyzed structure. A cruciform scatterer made of centrosymmetric materials (Au or Si) sits atop a glass substrate lying in the xy-plane. The gold cross has dimensions of L = 100 nm, W = 55 nm, and H = 30 nm, whereas the silicon cross has dimensions of L = 370 nm, W = 220 nm, and H = 220 nm. The cross is illuminated with a plane wave impinging normally onto the substrate, with the electric and magnetic fields being oriented along the arms of the cross. Hence, for the purposes of our calculations, we set θ = π and ϕ = π/2.

Figure 2

Linear spectral properties of gold crosses. (a) The spectra of the linear scattering cross-section of a cross made of gold, determined for different scaling values, α. (b) A more detailed understanding of the linear regime for the case α = 1 is provided by the spectra of the total radiated power and the power radiated by the electric dipole of the cross. The inset shows the electric field distribution calculated at the resonance wavelength in the xz-plane passing through the center of the cross.

Figure 3

Linear spectral properties of silicon crosses. (a) The spectra of the linear scattering cross-section of a silicon cross, determined for different scaling values, α. (b) A more detailed understanding of the linear regime for the case α = 1 is provided by the spectra of the total radiated power and the power radiated by the electric dipole and magnetic dipole of the cross. (c) Near-field distributions determined at the main resonances. Resonances A and C are primarily of electric dipole and magnetic dipole type, respectively, whereas additional terms must be considered to accurately describe resonance B. Note also that there is a small contribution to resonance A from a magnetic dipole. From left to right, bottom panels show the electric field distribution at the resonances A, B, and C, in the xz-plane passing through the center of the cross.

Figure 4

Spectral properties of surface second-harmonic generation in gold and silicon crosses. (a) The spectra of the power radiated at the second-harmonic by the nonlinear surface sources induced in a cross made of gold, determined for different scaling values, α. (b) The same as in (a) but calculated for crosses made of silicon. A log scale is chosen for the Au case to help highlight the resonances.

Figure 5

Spectral properties of bulk second-harmonic generation in gold and silicon crosses. (a) The spectra of the power radiated at the second-harmonic by the nonlinear bulk sources induced in a cross made of gold, determined for different scaling values, α. (b) The same as in (a) but calculated for crosses made of silicon. A log scale is chosen for the Au case to help highlight the resonances.

Figure 6

Relative contribution of surface and bulk to second-harmonic generation in gold and silicon crosses. (a) The dependence of the ratio κ = P_s/P_b between the SH powers generated by the surface and bulk nonlinear sources induced in a cross made of gold, determined for different scaling values, α. (b) The same as in (a) but calculated for the crosses made of silicon. (c) The value of the ratio κ evaluated at the wavelength at which the bulk contribution is maximum vs. the scaling parameter α, calculated for the crosses made of gold. (d) The same as in (c) but calculated for the crosses made of silicon.