A Finite Element Solution of Lateral Periodic Poisson-Boltzmann Model for Membrane Channel Proteins

Abstract

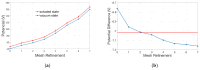
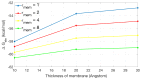
Membrane channel proteins control the diffusion of ions across biological membranes. They are closely related to the processes of various organizational mechanisms, such as: cardiac impulse, muscle contraction and hormone secretion. Introducing a membrane region into implicit solvation models extends the ability of the Poisson-Boltzmann (PB) equation to handle membrane proteins. The use of lateral periodic boundary conditions can properly simulate the discrete distribution of membrane proteins on the membrane plane and avoid boundary effects, which are caused by the finite box size in the traditional PB calculations. In this work, we: (1) develop a first finite element solver (FEPB) to solve the PB equation with a two-dimensional periodicity for membrane channel proteins, with different numerical treatments of the singular charges distributions in the channel protein; (2) add the membrane as a dielectric slab in the PB model, and use an improved mesh construction method to automatically identify the membrane channel/pore region even with a tilt angle relative to the z-axis; and (3) add a non-polar solvation energy term to complete the estimation of the total solvation energy of a membrane protein. A mesh resolution of about 0.25 Å (cubic grid space)/0.36 Å (tetrahedron edge length) is found to be most accurate in linear finite element calculation of the PB solvation energy. Computational studies are performed on a few exemplary molecules. The results indicate that all factors, the membrane thickness, the length of periodic box, membrane dielectric constant, pore region dielectric constant, and ionic strength, have individually considerable influence on the solvation energy of a channel protein. This demonstrates the necessity to treat all of those effects in the PB model for membrane protein simulations.

Keywords: finite element method; laterally periodic Poisson-Boltzmann model; membrane channel proteins; pore region; solvation.

Figure 1

A 2D schematic picture for the cross section of an ion channel system. The solvent region is labeled 1, the membrane channel protein is labeled 2 and the membrane is labeled 3. The solvent part between the white dotted lines is the channel region [29].

Figure 2

Relationship between the relative error and the times of mesh refinement: (a) single atom model represented by a singular point charge at the center; and (b) single atom model represented by a uniform charge distribution in the unit sphere.

Figure 3

Relationship between the potential at the position of the singular charge in the single atom model and the times of mesh refinement: (a) potentials in the solvated state and reference state (vacuum state); and (b) the difference of two potentials in (a).

Figure 4

Calculation results of electrostatic solvation energies by different boundary conditions and potential calculation methods vs. the size of box. The red line denotes periodic boundary condition with non-decomposition method; the green line denotes using Dirichlet boundary condition with non-decomposition method; the blue line denotes using Dirichlet boundary condition with decomposition method.

Figure 5

Sectional drawing of gA channel surface mesh. The molecular surface is shown in red, the membrane region is shown in blue, the solvent region is shown in green and yellow. Dark green and purple indicate the top and bottom of the box.

Figure 6

The solvation energy changes with the dielectric coefficient at the membrane region in different ionic strengths.

Figure 7

The relationship between the thickness of membrane and electrostatic solvation energy with a box size of $50\times 50\times 50$ Å${}^3$ with period boundary condition. The relative dielectric constant in membrane is set to 1 (in blue), 2 (in red), 4 (in yellow), and 8 (in green), respectively.

Figure 8

The effect of membrane in channel region on electrostatic solvation energy. The incorrectly added membrane is put into the channel region on the base of original ion channel model (in green). The thickness of the added membrane in the pore region (HMP) is 30, 20, and 10 Å, respectively. The original ion channel is equivalent to the case HMP = 0.

Figure 9

The solvation energy changes with the change of the tilt angle.

Figure 10

The treatment of the face gird in the direction of the periodic boundary conditions for the finite element method (FEM).

Figure 11

Volume mesh of gramicidin A (gA): (a) Wire-frame of volume mesh conforming to the boundary of a channel protein and membrane system; (b) the surface mesh of the membrane-protein region; and (c) the upper boundary surface of the membrane-protein region, in which the membrane is represented as a slab [29].

Figure 12

Four vertices of the tetrahedron are used as control points. E represents a random point inside the tetrahedron. ${\lambda }_2$ for E denotes the volumetric ratio of the yellow tetrahedron ($E{A}_1{A}_3{A}_4$) to the entire tetrahedron ($A_1{A}_2{A}_3{A}_4$). The same applies to ${\lambda }_1,{\lambda }_3,{\lambda }_4$.