Therapeutic target discovery using Boolean network attractors: improvements of kali
- PMID: 29515890
- PMCID: PMC5830779
- DOI: 10.1098/rsos.171852
Therapeutic target discovery using Boolean network attractors: improvements of kali
Abstract
In a previous article, an algorithm for identifying therapeutic targets in Boolean networks modelling pathological mechanisms was introduced. In the present article, the improvements made on this algorithm, named kali, are described. These improvements are (i) the possibility to work on asynchronous Boolean networks, (ii) a finer assessment of therapeutic targets and (iii) the possibility to use multivalued logic. kali assumes that the attractors of a dynamical system, such as a Boolean network, are associated with the phenotypes of the modelled biological system. Given a logic-based model of pathological mechanisms, kali searches for therapeutic targets able to reduce the reachability of the attractors associated with pathological phenotypes, thus reducing their likeliness. kali is illustrated on an example network and used on a biological case study. The case study is a published logic-based model of bladder tumorigenesis from which kali returns consistent results. However, like any computational tool, kali can predict but cannot replace human expertise: it is a supporting tool for coping with the complexity of biological systems in the field of drug discovery.
Keywords: Boolean network; attractor; biological network; bladder cancer; drug discovery; therapeutic target.
Conflict of interest statement
The authors declare that they have no competing interests.
Figures
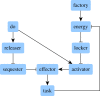
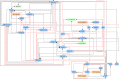
Similar articles
-
An in silico target identification using Boolean network attractors: Avoiding pathological phenotypes.C R Biol. 2014 Dec;337(12):661-78. doi: 10.1016/j.crvi.2014.10.002. Epub 2014 Nov 11. C R Biol. 2014. PMID: 25433558
-
An efficient algorithm for identifying primary phenotype attractors of a large-scale Boolean network.BMC Syst Biol. 2016 Oct 7;10(1):95. doi: 10.1186/s12918-016-0338-4. BMC Syst Biol. 2016. PMID: 27717349 Free PMC article.
-
P_UNSAT approach of attractor calculation for Boolean gene regulatory networks.J Theor Biol. 2018 Jun 14;447:171-177. doi: 10.1016/j.jtbi.2018.03.037. Epub 2018 Mar 29. J Theor Biol. 2018. PMID: 29605228
-
Attractor detection and enumeration algorithms for Boolean networks.Comput Struct Biotechnol J. 2022 May 21;20:2512-2520. doi: 10.1016/j.csbj.2022.05.027. eCollection 2022. Comput Struct Biotechnol J. 2022. PMID: 35685366 Free PMC article. Review.
-
Boolean modeling techniques for protein co-expression networks in systems medicine.Expert Rev Proteomics. 2016 Jun;13(6):555-69. doi: 10.1080/14789450.2016.1181546. Epub 2016 May 6. Expert Rev Proteomics. 2016. PMID: 27105325 Review.
Cited by
-
Complex networks interactions between bioactive compounds and adipose tissue vis-à-vis insulin resistance.Front Endocrinol (Lausanne). 2025 May 13;16:1578552. doi: 10.3389/fendo.2025.1578552. eCollection 2025. Front Endocrinol (Lausanne). 2025. PMID: 40433407 Free PMC article.
-
Boolean modelling as a logic-based dynamic approach in systems medicine.Comput Struct Biotechnol J. 2022 Jun 17;20:3161-3172. doi: 10.1016/j.csbj.2022.06.035. eCollection 2022. Comput Struct Biotechnol J. 2022. PMID: 35782730 Free PMC article. Review.
-
Multi-parameter exploration of dynamics of regulatory networks.Biosystems. 2020 Apr;190:104113. doi: 10.1016/j.biosystems.2020.104113. Epub 2020 Feb 10. Biosystems. 2020. PMID: 32057819 Free PMC article. Review.
-
Cohort-specific boolean models highlight different regulatory modules during Parkinson's disease progression.iScience. 2024 Sep 14;27(10):110956. doi: 10.1016/j.isci.2024.110956. eCollection 2024 Oct 18. iScience. 2024. PMID: 39429779 Free PMC article.
-
Data-Driven Modeling of Breast Cancer Tumors Using Boolean Networks.Front Big Data. 2021 Oct 20;4:656395. doi: 10.3389/fdata.2021.656395. eCollection 2021. Front Big Data. 2021. PMID: 34746770 Free PMC article.
References
-
- Poret A, Boissel J-P. 2014. An in silico target identification using Boolean network attractors: avoiding pathological phenotypes. C. R. Biol. 337, 661–678. (doi:10.1016/j.crvi.2014.10.002) - DOI - PubMed
-
- Le Novere N. 2015. Quantitative and logic modelling of molecular and gene networks. Nat. Rev. Genet. 16, 146–158. (doi:10.1038/nrg3885) - DOI - PMC - PubMed
-
- Wynn ML, Consul N, Merajver SD, Schnell S. 2012. Logic-based models in systems biology: a predictive and parameter-free network analysis method. Integr. Biol. (Camb) 4, 1323–1337. (doi:10.1039/c2ib20193c) - DOI - PMC - PubMed
-
- Morris MK, Saez-Rodriguez J, Sorger PK, Lauffenburger DA. 2010. Logic-based models for the analysis of cell signaling networks. Biochemistry 49, 3216–3224. (doi:10.1021/bi902202q) - DOI - PMC - PubMed
-
- Albert R, Thakar J. 2014. Boolean modeling: a logic-based dynamic approach for understanding signaling and regulatory networks and for making useful predictions. Wiley Interdiscip. Rev.: Syst. Biol. Med. 6, 353–369. (doi:10.1002/wsbm.1273) - DOI - PubMed
Associated data
LinkOut - more resources
Full Text Sources
Other Literature Sources

