CRISPR-based herd immunity can limit phage epidemics in bacterial populations
- PMID: 29521625
- PMCID: PMC5922976
- DOI: 10.7554/eLife.32035
CRISPR-based herd immunity can limit phage epidemics in bacterial populations
Abstract
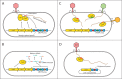
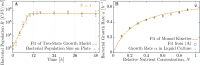
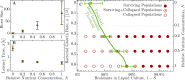
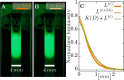
Herd immunity, a process in which resistant individuals limit the spread of a pathogen among susceptible hosts has been extensively studied in eukaryotes. Even though bacteria have evolved multiple immune systems against their phage pathogens, herd immunity in bacteria remains unexplored. Here we experimentally demonstrate that herd immunity arises during phage epidemics in structured and unstructured Escherichia coli populations consisting of differing frequencies of susceptible and resistant cells harboring CRISPR immunity. In addition, we develop a mathematical model that quantifies how herd immunity is affected by spatial population structure, bacterial growth rate, and phage replication rate. Using our model we infer a general epidemiological rule describing the relative speed of an epidemic in partially resistant spatially structured populations. Our experimental and theoretical findings indicate that herd immunity may be important in bacterial communities, allowing for stable coexistence of bacteria and their phages and the maintenance of polymorphism in bacterial immunity.
Keywords: CRISPR; E. coli; bacteria; ecology; epidemic; evolutionary biology; genomics; herd immunity; phage; polymorphism.
© 2018, Payne et al.
Conflict of interest statement
PP, LG, NB, JB No competing interests declared
Figures




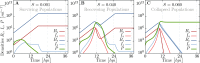
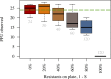

Similar articles
-
Coevolution between bacterial CRISPR-Cas systems and their bacteriophages.Cell Host Microbe. 2021 May 12;29(5):715-725. doi: 10.1016/j.chom.2021.03.018. Cell Host Microbe. 2021. PMID: 33984274 Review.
-
Why put up with immunity when there is resistance: an excursion into the population and evolutionary dynamics of restriction-modification and CRISPR-Cas.Philos Trans R Soc Lond B Biol Sci. 2019 May 13;374(1772):20180096. doi: 10.1098/rstb.2018.0096. Philos Trans R Soc Lond B Biol Sci. 2019. PMID: 30905282 Free PMC article.
-
The effect of phage genetic diversity on bacterial resistance evolution.ISME J. 2020 Mar;14(3):828-836. doi: 10.1038/s41396-019-0577-7. Epub 2020 Jan 2. ISME J. 2020. PMID: 31896785 Free PMC article.
-
Nasty viruses, costly plasmids, population dynamics, and the conditions for establishing and maintaining CRISPR-mediated adaptive immunity in bacteria.PLoS Genet. 2010 Oct 28;6(10):e1001171. doi: 10.1371/journal.pgen.1001171. PLoS Genet. 2010. PMID: 21060859 Free PMC article.
-
The Significance of Mutualistic Phages for Bacterial Ecology and Evolution.Trends Microbiol. 2016 Jun;24(6):440-449. doi: 10.1016/j.tim.2015.12.009. Epub 2016 Jan 27. Trends Microbiol. 2016. PMID: 26826796 Review.
Cited by
-
Long-run bacteria-phage coexistence dynamics under natural habitat conditions in an environmental biotechnology system.ISME J. 2021 Mar;15(3):636-648. doi: 10.1038/s41396-020-00802-z. Epub 2020 Oct 16. ISME J. 2021. PMID: 33067586 Free PMC article.
-
Mucin induces CRISPR-Cas defense in an opportunistic pathogen.Nat Commun. 2022 Jun 25;13(1):3653. doi: 10.1038/s41467-022-31330-3. Nat Commun. 2022. PMID: 35752617 Free PMC article.
-
The role of spatial structure in the evolution of viral innate immunity evasion: A diffusion-reaction cellular automaton model.PLoS Comput Biol. 2020 Feb 10;16(2):e1007656. doi: 10.1371/journal.pcbi.1007656. eCollection 2020 Feb. PLoS Comput Biol. 2020. PMID: 32040504 Free PMC article.
-
Ecological drivers of CRISPR immune systems.mSystems. 2024 Dec 17;9(12):e0056824. doi: 10.1128/msystems.00568-24. Epub 2024 Nov 6. mSystems. 2024. PMID: 39503509 Free PMC article.
-
Spatial structure affects phage efficacy in infecting dual-strain biofilms of Pseudomonas aeruginosa.Commun Biol. 2019 Nov 4;2:405. doi: 10.1038/s42003-019-0633-x. eCollection 2019. Commun Biol. 2019. PMID: 31701033 Free PMC article.
References
-
- Abramowitz M, Stegun IA. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. Vol. 55. Courier Corporation; 1964.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

