In silico study of multicellular automaticity of heterogeneous cardiac cell monolayers: Effects of automaticity strength and structural linear anisotropy
- PMID: 29529023
- PMCID: PMC5877903
- DOI: 10.1371/journal.pcbi.1005978
In silico study of multicellular automaticity of heterogeneous cardiac cell monolayers: Effects of automaticity strength and structural linear anisotropy
Abstract
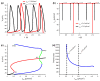
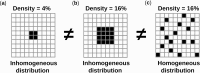
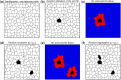
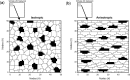
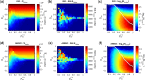
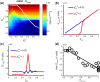
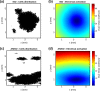
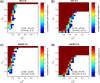
The biological pacemaker approach is an alternative to cardiac electronic pacemakers. Its main objective is to create pacemaking activity from added or modified distribution of spontaneous cells in the myocardium. This paper aims to assess how automaticity strength of pacemaker cells (i.e. their ability to maintain robust spontaneous activity with fast rate and to drive neighboring quiescent cells) and structural linear anisotropy, combined with density and spatial distribution of pacemaker cells, may affect the macroscopic behavior of the biological pacemaker. A stochastic algorithm was used to randomly distribute pacemaker cells, with various densities and spatial distributions, in a semi-continuous mathematical model. Simulations of the model showed that stronger automaticity allows onset of spontaneous activity for lower densities and more homogeneous spatial distributions, displayed more central foci, less variability in cycle lengths and synchronization of electrical activation for similar spatial patterns, but more variability in those same variables for dissimilar spatial patterns. Compared to their isotropic counterparts, in silico anisotropic monolayers had less central foci and displayed more variability in cycle lengths and synchronization of electrical activation for both similar and dissimilar spatial patterns. The present study established a link between microscopic structure and macroscopic behavior of the biological pacemaker, and may provide crucial information for optimized biological pacemaker therapies.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
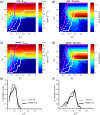
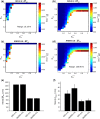

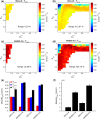
References
-
- Mangoni ME, Nargeot J. Genesis and Regulation of the Heart Automaticity. Physiol Rev. 2008;88: 919–982. doi: 10.1152/physrev.00018.2007 - DOI - PubMed
-
- Rozanski GJ, Lipsius SL. Electrophysiology of functional subsidiary pacemakers in canine right atrium. Am J Physiol. 1985;249: H594–603. doi: 10.1152/ajpheart.1985.249.3.H594 - DOI - PubMed
-
- Monfredi O, Maltsev VA, Lakatta EG. Modern Concepts Concerning the Origin of the Heartbeat. Physiology. 2013;28: 74–92. doi: 10.1152/physiol.00054.2012 - DOI - PMC - PubMed
-
- Maltsev VA, Lakatta EG. Dynamic interactions of an intracellular Ca2+ clock and membrane ion channel clock underlie robust initiation and regulation of cardiac pacemaker function. Cardiovasc Res. 2008;77: 274–284. doi: 10.1093/cvr/cvm058 - DOI - PubMed
-
- Maltsev VA, Vinogradova TM, Lakatta EG. The Emergence of a General Theory of the Initiation and Strength of the Heartbeat. J Pharmacol Sci. 2006;100: 338–369. doi: 10.1254/jphs.CR0060018 - DOI - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

