Gap junction plasticity as a mechanism to regulate network-wide oscillations
- PMID: 29529034
- PMCID: PMC5864095
- DOI: 10.1371/journal.pcbi.1006025
Gap junction plasticity as a mechanism to regulate network-wide oscillations
Abstract
Cortical oscillations are thought to be involved in many cognitive functions and processes. Several mechanisms have been proposed to regulate oscillations. One prominent but understudied mechanism is gap junction coupling. Gap junctions are ubiquitous in cortex between GABAergic interneurons. Moreover, recent experiments indicate their strength can be modified in an activity-dependent manner, similar to chemical synapses. We hypothesized that activity-dependent gap junction plasticity acts as a mechanism to regulate oscillations in the cortex. We developed a computational model of gap junction plasticity in a recurrent cortical network based on recent experimental findings. We showed that gap junction plasticity can serve as a homeostatic mechanism for oscillations by maintaining a tight balance between two network states: asynchronous irregular activity and synchronized oscillations. This homeostatic mechanism allows for robust communication between neuronal assemblies through two different mechanisms: transient oscillations and frequency modulation. This implies a direct functional role for gap junction plasticity in information transmission in cortex.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
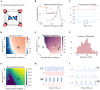
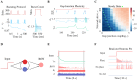
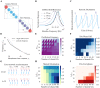
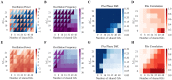
Similar articles
-
Distal gap junctions and active dendrites can tune network dynamics.J Neurophysiol. 2006 Mar;95(3):1669-82. doi: 10.1152/jn.00662.2005. Epub 2005 Dec 7. J Neurophysiol. 2006. PMID: 16339003
-
Beyond plasticity: the dynamic impact of electrical synapses on neural circuits.Nat Rev Neurosci. 2019 May;20(5):253-271. doi: 10.1038/s41583-019-0133-5. Nat Rev Neurosci. 2019. PMID: 30824857 Review.
-
Slow Dynamics in Microcolumnar Gap Junction Network of Developing Neocortical Pyramidal Neurons.Neuroscience. 2019 May 15;406:554-562. doi: 10.1016/j.neuroscience.2019.02.013. Epub 2019 Feb 20. Neuroscience. 2019. PMID: 30794844
-
The contribution of electrical synapses to field potential oscillations in the hippocampal formation.Front Neural Circuits. 2014 Apr 3;8:32. doi: 10.3389/fncir.2014.00032. eCollection 2014. Front Neural Circuits. 2014. PMID: 24772068 Free PMC article. Review.
-
The Potential Role of Gap Junctional Plasticity in the Regulation of State.Neuron. 2017 Mar 22;93(6):1275-1295. doi: 10.1016/j.neuron.2017.02.041. Neuron. 2017. PMID: 28334604 Review.
Cited by
-
Exacerbation of Epilepsy by Astrocyte Alkalization and Gap Junction Uncoupling.J Neurosci. 2021 Mar 10;41(10):2106-2118. doi: 10.1523/JNEUROSCI.2365-20.2020. Epub 2021 Jan 21. J Neurosci. 2021. PMID: 33478985 Free PMC article.
-
Cellular basis of learning and memory in the carotid body.Front Synaptic Neurosci. 2022 Aug 15;14:902319. doi: 10.3389/fnsyn.2022.902319. eCollection 2022. Front Synaptic Neurosci. 2022. PMID: 36046221 Free PMC article. Review.
-
Gabaergic Interneurons in Early Brain Development: Conducting and Orchestrated by Cortical Network Activity.Front Mol Neurosci. 2022 Jan 3;14:807969. doi: 10.3389/fnmol.2021.807969. eCollection 2021. Front Mol Neurosci. 2022. PMID: 35046773 Free PMC article.
-
Emergence of dynamic properties in network hypermotifs.Proc Natl Acad Sci U S A. 2022 Aug 9;119(32):e2204967119. doi: 10.1073/pnas.2204967119. Epub 2022 Aug 1. Proc Natl Acad Sci U S A. 2022. PMID: 35914142 Free PMC article.
-
Coherence and cognition in the cortex: the fundamental role of parvalbumin, myelin, and the perineuronal net.Brain Struct Funct. 2021 Sep;226(7):2041-2055. doi: 10.1007/s00429-021-02327-3. Epub 2021 Jun 27. Brain Struct Funct. 2021. PMID: 34175994 Review.
References
-
- Timofeev I, Bazhenov M, Seigneur J, Sejnowski T. Neuronal Synchronization and Thalamocortical Rhythms in Sleep, Wake and Epilepsy. Jasper’s Basic Mechanisms of the Epilepsies [Internet]. 2012; p. 1–24. - PubMed
-
- Buzsáki G. Theta Oscillations in the Hippocampus. Neuron. 2002;33(3):325–340. doi: 10.1016/S0896-6273(02)00586-X - DOI - PubMed
-
- Fries P. Modulation of Oscillatory Neuronal Synchronization by Selective Visual Attention. Science. 2001;291(5508):1560–1563. doi: 10.1126/science.1055465 - DOI - PubMed
-
- Gregoriou GG, Gotts SJ, Zhou H, Desimone R. High-frequency, long-range coupling between prefrontal and visual cortex during attention. Science (New York, NY). 2009;324(5931):1207–1210. doi: 10.1126/science.1171402 - DOI - PMC - PubMed
-
- Vinck M, Womelsdorf T, Buffalo EA, Desimone R, Fries P. Attentional modulation of cell-class-specific gamma-band synchronization in awake monkey area v4. Neuron. 2013;80(4):1077–1089. doi: 10.1016/j.neuron.2013.08.019 - DOI - PMC - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases
Miscellaneous

