Predicting drug resistance evolution: insights from antimicrobial peptides and antibiotics
- PMID: 29540517
- PMCID: PMC5879628
- DOI: 10.1098/rspb.2017.2687
Predicting drug resistance evolution: insights from antimicrobial peptides and antibiotics
Abstract
Antibiotic resistance constitutes one of the most pressing public health concerns. Antimicrobial peptides (AMPs) of multicellular organisms are considered part of a solution to this problem, and AMPs produced by bacteria such as colistin are last-resort drugs. Importantly, AMPs differ from many antibiotics in their pharmacodynamic characteristics. Here we implement these differences within a theoretical framework to predict the evolution of resistance against AMPs and compare it to antibiotic resistance. Our analysis of resistance evolution finds that pharmacodynamic differences all combine to produce a much lower probability that resistance will evolve against AMPs. The finding can be generalized to all drugs with pharmacodynamics similar to AMPs. Pharmacodynamic concepts are familiar to most practitioners of medical microbiology, and data can be easily obtained for any drug or drug combination. Our theoretical and conceptual framework is, therefore, widely applicable and can help avoid resistance evolution if implemented in antibiotic stewardship schemes or the rational choice of new drug candidates.
Keywords: antibiotics; antimicrobial peptides; pharmacodynamics; resistance evolution.
© 2018 The Author(s).
Conflict of interest statement
We declare we do not have competing interests.
Figures
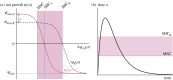
 . (b) Following the original approach to define the MSW [13], the boundaries of the MSW can also be applied to the pharmacokinetics of the system. The black line represents the change in antimicrobial concentration over time due to input (increase) and decay (decrease). The lower and upper boundaries of the shaded area indicate the MSW.
. (b) Following the original approach to define the MSW [13], the boundaries of the MSW can also be applied to the pharmacokinetics of the system. The black line represents the change in antimicrobial concentration over time due to input (increase) and decay (decrease). The lower and upper boundaries of the shaded area indicate the MSW.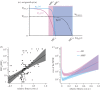
 .We plotted the size of the MSW (line) and the 95% CIs for both AMP-like and antibiotic (AB)-like pharmacodynamics, with ψmax,S = 1, MICS = 1, ψmin,S,AB = −5, ψmin,S,AMP = −50, κS,AB = 1.5 and κS,AMP = 5. ψmax,R was calculated using the relationship log10(MICR/MICS) = 2.59c + 1.65.
.We plotted the size of the MSW (line) and the 95% CIs for both AMP-like and antibiotic (AB)-like pharmacodynamics, with ψmax,S = 1, MICS = 1, ψmin,S,AB = −5, ψmin,S,AMP = −50, κS,AB = 1.5 and κS,AMP = 5. ψmax,R was calculated using the relationship log10(MICR/MICS) = 2.59c + 1.65.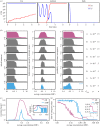
 μAMP = 3 × 10−7, ka = 0.5, ke = 0.2, dn = 0.01, τ = 1/24.
μAMP = 3 × 10−7, ka = 0.5, ke = 0.2, dn = 0.01, τ = 1/24.References
-
- World Health Organization. 2014. The evolving threat of antimicrobial resistance: options for action. Geneva, Switzerland: WHO.
Publication types
MeSH terms
Substances
Associated data
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
