Dynamic Group Multi-party Quantum Key Agreement

Abstract

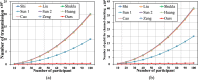
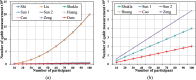
This paper presents a novel dynamic group multi-party Quantum Key Agreement (DGMQKA) protocol, achieved by a multicast transmission method. The proposed method is able to achieve arbitrary number of groups and members under the same resources. In addition, it can be dynamically adjusted by joining a new member, combining two groups into one group, revoking an old member and dividing one group into two groups, for different and complex situations. Furthermore, the proposed protocol can be of help to research into Quantum Secret Sharing (QSS), which it complements. The security analysis shows that the proposed protocol can resist both external and internal attacks. In consumption comparison, the proposed protocol using the multicast transmission method is more effective than other current MQKA protocols.

Figure 1

The procedure of two-group DGMQKA step 3. (a) The process of odd group, (b) The qubit states after operations.

Figure 2

The final states of two group example.

Figure 3

(a) Comparison of number of transmission: ours and references^–,–, (b) Comparison of number of qubit for channel checking: ours and references^–,–.

Figure 4

Comparison of number of qubit measurement: (a) Comparisons between our protocol and references^–,–, (b) Comparisons between our protocol and references^,– (enlarged Fig. 4a).