Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2018 Mar 1:12:122.
doi: 10.3389/fnins.2018.00122. eCollection 2018.

The Energy Coding of a Structural Neural Network Based on the Hodgkin-Huxley Model

Zhenyu Zhu  1 , Rubin Wang  1 , Fengyun Zhu  1
Affiliations

The Energy Coding of a Structural Neural Network Based on the Hodgkin-Huxley Model

Zhenyu Zhu et al. Front Neurosci. .

Abstract

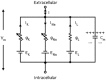
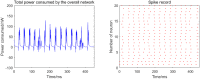
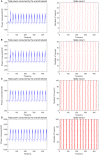
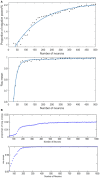
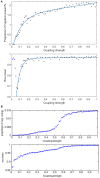
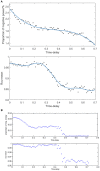
Based on the Hodgkin-Huxley model, the present study established a fully connected structural neural network to simulate the neural activity and energy consumption of the network by neural energy coding theory. The numerical simulation result showed that the periodicity of the network energy distribution was positively correlated to the number of neurons and coupling strength, but negatively correlated to signal transmitting delay. Moreover, a relationship was established between the energy distribution feature and the synchronous oscillation of the neural network, which showed that when the proportion of negative energy in power consumption curve was high, the synchronous oscillation of the neural network was apparent. In addition, comparison with the simulation result of structural neural network based on the Wang-Zhang biophysical model of neurons showed that both models were essentially consistent.

Keywords: energy distribution; negative energy; neural energy coding; power consumption curve; synchronous oscillation.

PubMed Disclaimer

Figures

Figure 1
Figure 1
The equivalent circuit diagram of the Hodgkin–Huxley model.
Figure 2
Figure 2
The action potential and corresponding power consumption curve.
Figure 3
Figure 3
The schematic of a fully connected structural neural network.
Figure 4
Figure 4
Total power consumed by the overall network of 20 neurons and the spike record under continuous stimulus. The coupling strength is uniformly distributed in [0, 0.5]; the signal transmitting delay is uniformly distributed in [0.3 ms, 1.8 ms].
Figure 5
Figure 5
The total power consumption and the spike record of the overall network under continuous stimulus. The number of neurons in (A–D) are 30, 50, 100, 200, respectively. The coupling strength is uniformly distributed in [0, 0.5]; the signal transmitting delay is uniformly distributed in [0.3 ms, 1.8 ms]. The periodicity of the total power consumption curve is increasingly apparent and the spike record exhibits clear streaks with the increasing size of the network which indicates the synchronization of neuronal activity is getting stronger.
Figure 6
Figure 6
The total power consumption and the spike record of the overall network under continuous stimulus. The distribution interval of the coupling strength in (A–E) are [0, 0.05], [0, 0.1], [0, 0.3], [0, 0.5], [0, 1], respectively. The number of neurons is 100 and the signal transmitting delay is uniformly distributed in [0.3 ms, 1.8 ms]. The periodicity of the total power consumption curve and the synchronization of the network are positively correlated to the coupling strength.
Figure 7
Figure 7
(A) The total power consumption and the spike record of the overall network under continuous stimulus. The distribution interval of the signal transmitting delay in (A–D) are [0.1 ms, 1.6 ms], [0.3 ms, 1.8 ms], [0.5 ms, 2.0 ms], [0.7 ms, 2.2 ms], respectively. The number of neurons is 100 and the coupling strength is uniformly distributed in [0, 1]. The periodicity of the total power consumption curve and the synchronization of the network are negatively correlated to the signal transmitting delay.
Figure 8
Figure 8
(A) The curve of α and ρmean varies as a function of the number of neurons in the network based on the Hodgkin–Huxley model; (B) The curves of α and ρmean vary as a function of the number of neurons in the network based on Wang–Zhang biophysics model (Wang et al., ; Wang and Wang, 2014).
Figure 9
Figure 9
(A) The curve of α and ρmean varies with different distribution intervals of coupling strength in the network based on the Hodgkin–Huxley model; (B) The curves of α and ρmean varies with different distribution intervals of coupling strength in the network based on Wang–Zhang biophysical model (Wang et al., ; Wang and Wang, 2014).
Figure 10
Figure 10
(A) The curve of α and ρmean varies with different distribution intervals of signal transmitting delay in the network based on the Hodgkin–Huxley model; (B) The curve of α and ρmean varies with different distribution intervals of signal transmitting delay in the network based on Wang–Zhang biophysical model (Wang et al., ; Wang and Wang, 2014).
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Abbott L. F. (2008). Theoretical neuroscience rising. Neuron 60, 489–495. 10.1016/j.neuron.2008.10.019 - DOI - PubMed
    1. Alle H., Roth A., Geiger J. R. P. (2009). Energy-efficient action potentials in hippocampal mossy fibers. Science 325, 1405–1408. 10.1126/science.1174331 - DOI - PubMed
    1. Amari S., Nakahara H. (2005). Difficulty of singularity in population coding. Neural Comput. 17, 839–858. 10.1162/0899766053429426 - DOI - PubMed
    1. Attwell D., Laughlin S. B. (2001). An energy budget for signaling in the grey matter of the brain. J. Cereb. Blood Flow Metab. 21, 1133–1145. 10.1097/00004647-200110000-00001 - DOI - PubMed
    1. Déli E., Tozzi A., Peters J. F. (2017). Relationships between short and fast brain timescales. Cogn. Neurodyn. 11, 539–552. 10.1007/s11571-017-9450-4 - DOI - PMC - PubMed

LinkOut - more resources