Archimedes' law explains penetration of solids into granular media
- PMID: 29549250
- PMCID: PMC5856792
- DOI: 10.1038/s41467-018-03344-3
Archimedes' law explains penetration of solids into granular media
Abstract
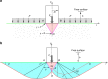
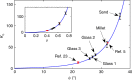
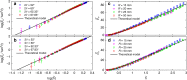
Understanding the response of granular matter to intrusion of solid objects is key to modelling many aspects of behaviour of granular matter, including plastic flow. Here we report a general model for such a quasistatic process. Using a range of experiments, we first show that the relation between the penetration depth and the force resisting it, transiently nonlinear and then linear, is scalable to a universal form. We show that the gradient of the steady-state part, K ϕ , depends only on the medium's internal friction angle, ϕ, and that it is nonlinear in μ = tan ϕ, in contrast to an existing conjecture. We further show that the intrusion of any convex solid shape satisfies a modified Archimedes' law and use this to: relate the zero-depth intercept of the linear part to K ϕ and the intruder's cross-section; explain the curve's nonlinear part in terms of the stagnant zone's development.
Conflict of interest statement
The authors declare no competing interests.
Figures




Similar articles
-
Support of modified Archimedes' law theory in granular media.Soft Matter. 2019 Apr 3;15(14):3008-3017. doi: 10.1039/c8sm02480d. Soft Matter. 2019. PMID: 30865192
-
Force and flow at the onset of drag in plowed granular media.Phys Rev E Stat Nonlin Soft Matter Phys. 2014 Apr;89(4):042202. doi: 10.1103/PhysRevE.89.042202. Epub 2014 Apr 3. Phys Rev E Stat Nonlin Soft Matter Phys. 2014. PMID: 24827236
-
Microstructure evolution during impact on granular matter.Phys Rev E Stat Nonlin Soft Matter Phys. 2012 Jan;85(1 Pt 1):011305. doi: 10.1103/PhysRevE.85.011305. Epub 2012 Jan 18. Phys Rev E Stat Nonlin Soft Matter Phys. 2012. PMID: 22400563
-
Shear-Jammed, Fragile, and Steady States in Homogeneously Strained Granular Materials.Phys Rev Lett. 2019 Oct 11;123(15):158001. doi: 10.1103/PhysRevLett.123.158001. Phys Rev Lett. 2019. PMID: 31702280
-
Review of the Functions of Archimedes' Spiral Metallic Nanostructures.Nanomaterials (Basel). 2017 Nov 22;7(11):405. doi: 10.3390/nano7110405. Nanomaterials (Basel). 2017. PMID: 29165382 Free PMC article. Review.
Cited by
-
Granular flow experiment using artificial gravity generator at International Space Station.NPJ Microgravity. 2023 Aug 8;9(1):61. doi: 10.1038/s41526-023-00308-w. NPJ Microgravity. 2023. PMID: 37553360 Free PMC article.
-
Virtual Energy Management for Physical Energy Savings in a Legged Robot Hopping on Granular Media.Front Robot AI. 2021 Dec 21;8:740927. doi: 10.3389/frobt.2021.740927. eCollection 2021. Front Robot AI. 2021. PMID: 34993236 Free PMC article.
-
Mechanistic framework for reduced-order models in soft materials: Application to three-dimensional granular intrusion.Proc Natl Acad Sci U S A. 2023 Jan 24;120(4):e2214017120. doi: 10.1073/pnas.2214017120. Epub 2023 Jan 17. Proc Natl Acad Sci U S A. 2023. PMID: 36649408 Free PMC article.
-
Detecting subtle subterranean movement via laser speckle imaging.J Exp Biol. 2024 Nov 15;227(22):jeb247267. doi: 10.1242/jeb.247267. Epub 2024 Nov 22. J Exp Biol. 2024. PMID: 39575697 Free PMC article.
-
Imperfect bodies sink imperfectly when settling in granular matter.Sci Adv. 2023 May 12;9(19):eadf6243. doi: 10.1126/sciadv.adf6243. Epub 2023 May 12. Sci Adv. 2023. PMID: 37172098 Free PMC article.
References
-
- Nagel SR. Experimental soft-matter science. Rev. Mod. Phys. 2017;89:025002. doi: 10.1103/RevModPhys.89.025002. - DOI
-
- Collins AL, et al. The effect of rod nose shape on the internal flow fields during the ballistic penetration of sand. Int. J. Impact Eng. 2011;38:951–963. doi: 10.1016/j.ijimpeng.2011.08.002. - DOI
-
- Aguilar, J. & Goldman, D. I. Robophysical study of jumping dynamics on granular media. Nat. Phys. 12, 278–283 (2016).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

