Archimedes' law explains penetration of solids into granular media

Abstract

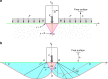
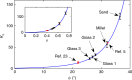
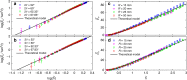
Understanding the response of granular matter to intrusion of solid objects is key to modelling many aspects of behaviour of granular matter, including plastic flow. Here we report a general model for such a quasistatic process. Using a range of experiments, we first show that the relation between the penetration depth and the force resisting it, transiently nonlinear and then linear, is scalable to a universal form. We show that the gradient of the steady-state part, K _ϕ , depends only on the medium's internal friction angle, ϕ, and that it is nonlinear in μ = tan ϕ, in contrast to an existing conjecture. We further show that the intrusion of any convex solid shape satisfies a modified Archimedes' law and use this to: relate the zero-depth intercept of the linear part to K _ϕ and the intruder's cross-section; explain the curve's nonlinear part in terms of the stagnant zone's development.

Fig. 1

Experimental setup and validation of the quasistatic regime. a Sketch of the experimental apparatus. An intruder is connected to the servo-controlled beam through a force sensor. The intruder is inserted into the granular medium at constant low velocity, while the vertical displacement and total vertical resistance force are continuously recorded. b The raw data for the vertical resistance force on a cylindrical of diameter D = 40 mm and length L = 50 mm, penetrating quartz sand with different velocities, ranging from 10 mm min⁻¹ to 300 mm min⁻¹. The independence of the velocity indicating the quasistatic state of the experiment. The red dashed line marks the end of the transient nonlinear regime

Fig. 2

Dimensionless pressure–depth curves for the different granular materials. a–c Glass beads 1–3, respectively; d quartz sand; e millet. The error bars represent standard deviations over samples, as detailed in the Methods section. Photos of the respective granular materials are shown in the lower right corners. f The parameters for the five granular materials: ρ_s is the packing mass density, d_g is the particle diameter and ϕ is the angle of repose, accurate to ±2°. The plots collapse very well for all the granular media, regardless of the intruder size. The nonlinear-to-linear crossover, shown by a vertical dashed line, is at a similar value in all the experiments: ${\tilde{h}}_0=0.15\pm 0.06$. The solid lines are linear fits to the experimental data for $\tilde{h}>0.15$. The fit quality is: R² >0.990, 0.977, 0.985, 0.996 and 0.935, respectively, for the glass beads types 1–3, the sand and the millet

Fig. 3

Independence of the force–depth curve of the intruder’s cross-section shape. a The cross-sections, normal to the direction of penetration, of the polygonal prisms used in the experiments. b Dimensionless pressure–depth curves for different polygon prisms penetrating glass beads 1. The black line is the fit in Fig. 2a; inset: a zoom in on the nonlinear regime. $\tilde{h}$ is measured in units of the equivalent radius, $R_{\mathrm{e}}=\sqrt{S\mathrm{∕}\pi }$. The measurements were taken on 3 samples for each shape and the error bars represent the standard deviation over the samples. The fits qualities are: R² >0.997, 0.992, 0.998, and 0.993, respectively, for the square, rectangle, equilateral triangle and right-angle triangle. The experimental data of all the polygon intruders collapse on the fitted curve in Fig. 2a for all the cylinders (solid line), suggesting the K_ϕ is a pure material constitutive parameter

Fig. 4

The theoretical model. a The system includes the intruder and a conical SZ ahead of it. b Examples of the “+” (red lines) and “−” (black lines) characteristic paths in the rz plane, as well as their dependence on the angle β = π/4 − ϕ/2. α = 0 at the intruder’s bottom and −π/2 at the cone surface

Fig. 5

Validation of the calculation of K_ϕ. K_ϕ, calculated from Eq. (5) (solid line), and its measured values. The black marks, from all our experiments, and the red mark, from refs. ^,, fall squarely on the predicted curve. Error bars represent one standard deviation about the mean. All our experimental values (black points) incur a horizontal error bar of ±2°, which was omitted to avoid clutter. Inset: the relationship between K_ϕ and μ = tanϕ is clearly superlinear, challenging the assumption of linearity in the LFFM. The error bars represent one standard deviation about the mean. Using the data reported in ref. , we estimate the internal friction angle of their poppy seed granules as 32.3° ± 0.3°. The quality of the fit between the experimental points and the theoretical curve is R² = 0.996

Fig. 6

Illustration of the non-flat intruders and the growth of the SZ. a A conical intruder. b A semi-spherical intruder. c A sketch of the development of the SZ ahead of a flat-bottom intruder. Note the change in the directions of the normal forces as the SZ evolves

Fig. 7

Intrusion of cones and spheres. a, b The rescaled force $\log \left({\tilde{p}}_u{\mathrm{∕tan}}^{\mathrm{2}}\theta \right)$ vs. $\log \tilde{h}$, measured from the intruder’s bottom, for conical intruders of different head angles 2θ penetrating glass beads 2 and 3. We normalise depth by R = 20 mm to coincide with our cylindrical intruders experiments. The experimental data are in good agreement with the theoretical calculation (solid lines), ${\tilde{p}}_u={\tan }^2\theta K_{\varphi }{\tilde{h}}^3\mathrm{∕}3$. c, d The same as in a, b for spherical intruders of different radii, penetrating glass beads 2 and 3. Again, the experimental data agree well with the theoretical curves (solid lines): ${\tilde{p}}_u=K_{\varphi }{\tilde{h}}^2\left(1-\tilde{h}\mathrm{∕}3\right)$ and ${\tilde{p}}_u=K_{\varphi }\left(\tilde{h}-1\mathrm{∕}3\right)$ for $\tilde{h}\le 1$ and $\tilde{h}>1$, respectively. All the measurements were taken on three samples for each of the four experiments, with the error bars representing the standard deviation over the samples. The fits qualities are: R² >0.991, 0.993, 0.993 and 0.995, respectively, for a–d