The influence of medium elasticity on the prediction of histotripsy-induced bubble expansion and erythrocyte viability
- PMID: 29553049
- PMCID: PMC5959013
- DOI: 10.1088/1361-6560/aab79b
The influence of medium elasticity on the prediction of histotripsy-induced bubble expansion and erythrocyte viability
Abstract
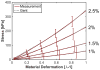
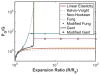
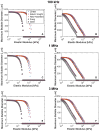
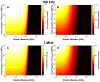
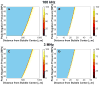
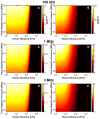
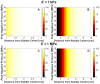
Histotripsy is a form of therapeutic ultrasound that liquefies tissue mechanically via acoustic cavitation. Bubble expansion is paramount in the efficacy of histotripsy therapy, and the cavitation dynamics are strongly influenced by the medium elasticity. In this study, an analytic model to predict histotripsy-induced bubble expansion in a fluid was extended to include the effects of medium elasticity. Good agreement was observed between the predictions of the analytic model and numerical computations utilizing highly nonlinear excitations (shock-scattering histotripsy) and purely tensile pulses (microtripsy). No bubble expansion was computed for either form of histotripsy when the elastic modulus was greater than 20 MPa and the peak negative pressure was less than 50 MPa. Strain in the medium due to the expansion of a single bubble was also tabulated. The viability of red blood cells was calculated as a function of distance from the bubble wall based on empirical data of impulsive stretching of erythrocytes. Red blood cells remained viable at distances further than 44 µm from the bubble wall. As the medium elasticity increased, the distance over which bubble expansion-induced strain influenced red blood cells was found to decrease sigmoidally. These results highlight the relationship between tissue elasticity and the efficacy of histotripsy. In addition, an upper medium elasticity limit was identified, above which histotripsy may not be effective for tissue liquefaction.
Figures
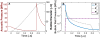





References
-
- Apfel RE. Acoustic cavitation prediction. J Acoust Soc Am. 1981a;69:1624–33.
-
- Apfel RE. Methods in Experimental Physics. Vol. 19. New York: Academic Press, Inc; 1981b. Acoustic Cavitation; pp. 355–411.
-
- Apfel RE. Possibility of microcavitation from diagnostic ultrasound. IEEE Trans Ultrason Ferro Freq Control. 1986;33:139–42. - PubMed
-
- Apfel RE, Holland CK. Gauging the likelihood of cavitation from short-pulse, low-duty cycle diagnostic ultrasound. Ultrasound Med Biol. 1991;17:179–85. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
