Scale matters

Abstract

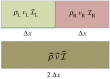
The applicability of Navier-Stokes equations is limited to near-equilibrium flows in which the gradients of density, velocity and energy are small. Here I propose an extension of the Chapman-Enskog approximation in which the velocity probability distribution function (PDF) is averaged in the coordinate phase space as well as the velocity phase space. I derive a PDF that depends on the gradients and represents a first-order generalization of local thermodynamic equilibrium. I then integrate this PDF to derive a hydrodynamic model. I discuss the properties of that model and its relation to the discrete equations of computational fluid dynamics.This article is part of the theme issue 'Hilbert's sixth problem'.

Keywords: coarse-graining; finite scale; high Reynolds number.

Figure 1.

The coarsening process consists of merging two cells with possibly different values of state variables density, velocity and internal energy into a single larger cell. Values of the state variables in the larger cell are constrained by conservation, but not completely determined by conservation. (Online version in colour.)