Language acquisition with communication between learners
- PMID: 29593089
- PMCID: PMC5908541
- DOI: 10.1098/rsif.2018.0073
Language acquisition with communication between learners
Abstract
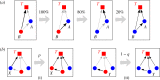
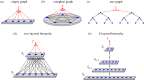
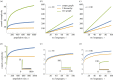
We consider a class of students learning a language from a teacher. The situation can be interpreted as a group of child learners receiving input from the linguistic environment. The teacher provides sample sentences. The students try to learn the grammar from the teacher. In addition to just listening to the teacher, the students can also communicate with each other. The students hold hypotheses about the grammar and change them if they receive counter evidence. The process stops when all students have converged to the correct grammar. We study how the time to convergence depends on the structure of the classroom by introducing and evaluating various complexity measures. We find that structured communication between students, although potentially introducing confusion, can greatly reduce some of the complexity measures. Our theory can also be interpreted as applying to the scientific process, where nature is the teacher and the scientists are the students.
Keywords: inductive inference; language learning; population structures in learning.
© 2018 The Author(s).
Conflict of interest statement
We declare we have no competing interests.
Figures

Similar articles
-
The evolutionary dynamics of grammar acquisition.J Theor Biol. 2001 Mar 7;209(1):43-59. doi: 10.1006/jtbi.2000.2240. J Theor Biol. 2001. PMID: 11237569
-
Win-stay, lose-shift in language learning from peers.Proc Natl Acad Sci U S A. 2004 Dec 28;101(52):18053-7. doi: 10.1073/pnas.0406608102. Epub 2004 Dec 16. Proc Natl Acad Sci U S A. 2004. PMID: 15604145 Free PMC article.
-
The Role of Simple Semantics in the Process of Artificial Grammar Learning.J Psycholinguist Res. 2017 Oct;46(5):1285-1308. doi: 10.1007/s10936-017-9494-y. J Psycholinguist Res. 2017. PMID: 28484966
-
Language learning from positive evidence, reconsidered: a simplicity-based approach.Top Cogn Sci. 2013 Jan;5(1):35-55. doi: 10.1111/tops.12005. Top Cogn Sci. 2013. PMID: 23335573 Review.
-
The growth of language: Universal Grammar, experience, and principles of computation.Neurosci Biobehav Rev. 2017 Oct;81(Pt B):103-119. doi: 10.1016/j.neubiorev.2016.12.023. Epub 2017 Jan 7. Neurosci Biobehav Rev. 2017. PMID: 28077259 Review.
References
-
- Lightfoot D. 1999. The development of language: acquisition, change, and evolution. Hoboken, New Jersey: Wiley-Blackwell.
-
- Wexler K, Culicover P. 1980. Formal principles of language acquisition. Cambridge, MA: MIT Press.
-
- Smith JM. 1982. Evolution and the theory of games. Cambridge, UK: Cambridge university press.
-
- Nowak MA. 2006. Evolutionary dynamics. Cambridge, MA: Harvard University Press.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

