Dynamics of Zika virus outbreaks: an overview of mathematical modeling approaches

Abstract

Background: The Zika virus was first discovered in 1947. It was neglected until a major outbreak occurred on Yap Island, Micronesia, in 2007. Teratogenic effects resulting in microcephaly in newborn infants is the greatest public health threat. In 2016, the Zika virus epidemic was declared as a Public Health Emergency of International Concern (PHEIC). Consequently, mathematical models were constructed to explicitly elucidate related transmission dynamics.

Survey methodology: In this review article, two steps of journal article searching were performed. First, we attempted to identify mathematical models previously applied to the study of vector-borne diseases using the search terms "dynamics," "mathematical model," "modeling," and "vector-borne" together with the names of vector-borne diseases including chikungunya, dengue, malaria, West Nile, and Zika. Then the identified types of model were further investigated. Second, we narrowed down our survey to focus on only Zika virus research. The terms we searched for were "compartmental," "spatial," "metapopulation," "network," "individual-based," "agent-based" AND "Zika." All relevant studies were included regardless of the year of publication. We have collected research articles that were published before August 2017 based on our search criteria. In this publication survey, we explored the Google Scholar and PubMed databases.

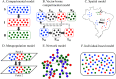
Results: We found five basic model architectures previously applied to vector-borne virus studies, particularly in Zika virus simulations. These include compartmental, spatial, metapopulation, network, and individual-based models. We found that Zika models carried out for early epidemics were mostly fit into compartmental structures and were less complicated compared to the more recent ones. Simple models are still commonly used for the timely assessment of epidemics. Nevertheless, due to the availability of large-scale real-world data and computational power, recently there has been growing interest in more complex modeling frameworks.

Discussion: Mathematical models are employed to explore and predict how an infectious disease spreads in the real world, evaluate the disease importation risk, and assess the effectiveness of intervention strategies. As the trends in modeling of infectious diseases have been shifting towards data-driven approaches, simple and complex models should be exploited differently. Simple models can be produced in a timely fashion to provide an estimation of the possible impacts. In contrast, complex models integrating real-world data require more time to develop but are far more realistic. The preparation of complicated modeling frameworks prior to the outbreaks is recommended, including the case of future Zika epidemic preparation.

Keywords: Deterministic; Epidemic model; Import risk; Intervention; Stochastic; Zika.

Figure 1. Conceptual frameworks of different epidemic models.

The colors represent epidemiological status: susceptible (S, blue), exposed (E, gray), infectious (I, red), and recovered (R, green). (A) Basic SIR compartmental model. Individuals are assumed to be well-mixed and are classified only according to their epidemiological status. (B) Vector-borne compartmental model. The subscripts H and M denote human and mosquito, respectively. Both host and vector individuals are assumed to be well-mixed and are classified only according to their epidemiological status. (C) Spatial model. Individuals are located at different locations. The transmission of infection between an infectious individual and a susceptible individual at distance x may occur with probability K(x). (D) Metapopulation model. The entire population is divided into two distinct subpopulations, each with independent disease transmission dynamics, together with interactions between subpopulations. The subpopulation in each patch is mixed homogeneously. (E) Network model. The model is formed by at least two basic components: vertex and edge. Vertices are connected by edges defined by the relationship of interest such as trade or travel. Infectious diseases are modeled to spread via the edges in this model. (F) Individual-based model. In this most complicated model, the stochastic epidemiological dynamics for each individual can be explicitly simulated with a set of characteristics including epidemiological status, spatial location, interaction preference, behavior traits, etc.