Instability of expanding bacterial droplets

Abstract

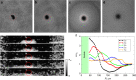
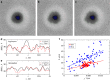
Suspensions of motile bacteria or synthetic microswimmers, termed active matter, manifest a remarkable propensity for self-organization, and formation of large-scale coherent structures. Most active matter research deals with almost homogeneous in space systems and little is known about the dynamics of strongly heterogeneous active matter. Here we report on experimental and theoretical studies on the expansion of highly concentrated bacterial droplets into an ambient bacteria-free fluid. The droplet is formed beneath a rapidly rotating solid macroscopic particle inserted in the suspension. We observe vigorous instability of the droplet reminiscent of a violent explosion. The phenomenon is explained in terms of continuum first-principle theory based on the swim pressure concept. Our findings provide insights into the dynamics of active matter with strong density gradients and significantly expand the scope of experimental and analytic tools for control and manipulation of active systems.

Fig. 1

Illustration of droplet instability. a Three-dimensional schematic representation of the experimental setup. A 60 μm nickel particle is spun by an external magnetic field inside a pendant drop with swimming bacteria. Rotation of the particle creates a vortex; the vortex redistributes bacteria and forms a dense bacterial droplet. b Stable bacterial concentration distribution for rotation frequency of 400 Hz. Scale bar is 50 μm. c Vigorous explosion of the concentrated bacterial droplet 1 s after cessation of rotation

Fig. 2

Fluorescence and tomography analysis. a–d Images of fluorescent bacteria in the vicinity of a rotating particle. White color corresponds to higher concentration of bacteria. Images are made from the bottom. The frequency of rotation is 160 Hz. a The initial distribution of live bacteria near the bottom of the film before the onset of rotation. b Uniform distribution of bacteria immediately after the onset of rotation. c Stationary distribution of swimming bacteria around the rotating particle. Bacteria are concentrated in the close proximity of the particle. Red dashed circles illustrate the size of the particle. d Distribution of dead (non-motile) bacteria remains uniform. Scale bar is 50 μm. e The OCT images showing bacterial distribution around the particle in a vertical cross-section at different moments of time after cessation of rotation. The OCT probe is scanning from the bottom. Bright white color corresponds to higher bacterial concentration, n_m = 10¹¹ cm⁻³. The bottom part of the spinning particle (dashed red circle) and concentrated bacteria are visible as a bright spot near the center of the first image. The droplet of concentrated bacteria is expanding along the bottom surface of the film in four consecutive images. Scale bar is 200 μm. f Averaged radial distributions of bacteria around the particle at different moments of time after cessation of rotation. n₀ is concentration of bacteria far from the particle

Fig. 3

Droplet's interface instability. The sequence of three consecutive snapshots illustrating the evolution of the dense droplet for times t = 0.15 s (a), t = 0.3 s (b), and t = 0.4 s (c) after cessation of rotation. The interface between dilute (bright) and dense (dark) regions is shown in green line. Rotation frequency is 400 Hz. Dependence of the interface velocity V (green) on the interface curvature (χ) for the exploding droplet 0.2 s after cessation of rotation. d, e Dependence of the interface velocity V (dashed red) and the interface curvature χ (solid black) on the polar angle φ for the experimental data (d) and the data obtained from simulations (e). A noticeable correlation between V and χ is observed both in experiments and simulations. f Parametric dependence of the interface normal velocity V vs curvature χ for experimental data (blue diamonds) and simulations (red circles). Two lines are linear regression fits

Fig. 4

Stagnation zone. a A stagnation zone formed by a sphere rotating around an axis perpendicular to a plane: stream surfaces in a plane containing the rotation axis for f = 400 Hz, radius of the particle a = 30 μm. Velocity is measured in mm s⁻¹. b Magnitude of the vortex velocity U_v vs frequency

Fig. 5

Expansion of a spot. a, b The onset of polar order (indicated by red arrow) from a slightly perturbed nematic state. c–e A sequence of gray-scale images illustrating expansion and instability of the dense spot for t = 2 (c), t = 25 (d), t = 34 (e) dimensionless time units after cessation of rotation. The nondimensional concentration field n is coded from white (n = 0) to black (max(n)). Initial spot radius is r₀ = 20, and initial nondimensional concentration is n = n₀ = 8. Outside the spot, the concentration is n = n₁ = 0.85, i.e., dimensional n < n_c. A depletion zone, seen as a bright halo, is imposed by initial conditions n = 0.2 in the domain r₀ < r < 2r₀, see panel (c). For the parameters of computational model see Methods section