Explained variation of excess hazard models

Abstract

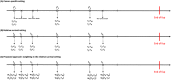
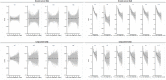
The availability of longstanding collection of detailed cancer patient information makes multivariable modelling of cancer-specific hazard of death appealing. We propose to report variation in survival explained by each variable that constitutes these models. We adapted the ranks explained (RE) measure to the relative survival data setting, ie, when competing risks of death are accounted for through life tables from the general population. RE is calculated at each event time. We introduce weights for each death reflecting its probability to be a cancer death. RE varies between -1 and +1 and can be reported at given times in the follow-up and as a time-varying measure from diagnosis onward. We present an application for patients diagnosed with colon or lung cancer in England. The RE measure shows reasonable properties and is comparable in both relative and cause-specific settings. One year after diagnosis, RE for the most complex excess hazard models reaches 0.56, 95% CI: 0.54 to 0.58 (0.58 95% CI: 0.56-0.60) and 0.69, 95% CI: 0.68 to 0.70 (0.67, 95% CI: 0.66-0.69) for lung and colon cancer men (women), respectively. Stage at diagnosis accounts for 12.4% (10.8%) of the overall variation in survival among lung cancer patients whereas it carries 61.8% (53.5%) of the survival variation in colon cancer patients. Variables other than performance status for lung cancer (10%) contribute very little to the overall explained variation. The proportion of the variation in survival explained by key prognostic factors is a crucial information toward understanding the mechanisms underpinning cancer survival. The time-varying RE provides insights into patterns of influence for strong predictors.

Keywords: excess hazard models; explained variation.

Figure 1

Calculation of RE in different settings (A) Cancer‐specific setting (B) Relative survival setting (C) Proposed approach: Weighting in the relative survival setting. ◯ time of cancer death; X time of non‐cancer death; | time of censoring; r_M: Rank as estimated from the model‐derived hazard of death; r₀: Average rank of the records in the risk set; r_P: 1; w_i: probability of cancer death [Colour figure can be viewed at http://wileyonlinelibrary.com]

Figure 2

Sum of weights and actual number of cancer deaths, for each of a 1000 simulated datasets, by cancer and simulation scenario. S1: Simulation scenario 1, linear proportional effect of age at diagnosis; S2: Simulation scenario 2, non‐linear non‐proportional effect of age, non‐proportional effects of categorical stage and deprivation [Colour figure can be viewed at http://wileyonlinelibrary.com]

Figure 3

Comparison of RE obtained in cause‐specific and relative survival settings, by cancer and simulation scenario

Figure 4

REw measured at 5 years, using different well‐specified (M1, M2, plain lines) and mis‐specified (M3‐M10) models, by cancer and simulation scenario. S1: Simulation scenario 1, linear proportional effect of age at diagnosis; M1: Linear proportional effect of age (plain line across M3‐M5); M3: Linear non‐proportional effect of age; M4: Non‐linear proportional effect of age; M5: Non‐linear non‐proportional effect of age; S2: Simulation scenario 2, non‐linear non‐proportional effect of age, non‐proportional effects of categorical stage and deprivation (plain line across M6‐M10); M2: Non‐linear non‐proportional effect of age, non‐proportional effects of categorical stage and deprivation; M6: Non‐linear non‐proportional effect of age, non‐proportional effect of categorical deprivation; M7: Non‐linear non‐proportional effect of age, non‐proportional effect of categorical stage; M8: Linear proportional effect of age, categorical stage and deprivation; M9: Non‐linear non‐proportional effect of age, proportional effect of categorical stage, non‐proportional effect of categorical deprivation; M10: Non‐linear non‐proportional effect of age, non‐proportional effect of categorical stage, proportional effect of categorical deprivation

Figure 5

Local REw measured up to 5 years, for different well‐specified (M1, M2) and mis‐specified models (M3‐M5 and M6‐M10): breast and lung cancers. S1: Simulation scenario 1, linear proportional effect of age at diagnosis; M1: Linear proportional effect of age; M3: Linear non‐proportional effect of age; M4: Non‐linear proportional effect of age; M5: Non‐linear non‐proportional effect of age; S2: Simulation scenario 2, non‐linear non‐proportional effect of age, non‐proportional effects of categorical stage and deprivation; M2: Non‐linear non‐proportional effect of age, non‐proportional effects of categorical stage and deprivation; M6: Non‐linear non‐proportional effect of age, non‐proportional effect of categorical deprivation; M7: Non‐linear non‐proportional effect of age, non‐proportional effect of categorical stage; M8: Linear proportional effect of age, categorical stage and deprivation; M9: Non‐linear non‐proportional effect of age, proportional effect of categorical stage, non‐proportional effect of categorical deprivation; M10: Non‐linear non‐proportional effect of age, non‐proportional effect of categorical stage, proportional effect of categorical deprivation

Figure 6

Multivariable models: (A) explained variation measured at 1 month and every 3 months after diagnosis, (B) smoothed local RE up to 3 years after diagnosis, for models adjusted for the effects of age and deprivation, and stage, and treatment. Colon cancer patients diagnosed in 2011 to 2013, selected for their valid stage at diagnosis: 4950 men and 4350 women the curve for comorbidity is not presented here as it is undistinguishable from the age and deprivation model Notes: (1) RE(t) and local RE can have values between −1 and +1 (2) Cumulative RE, RE(t) is calculated at month 1, 3, 6…36 after diagnosis (3) Local RE is calculated using information from 10 events on either side of the index event. The smoothed (lowess with mean smoother) curve is presented here

Figure 7

Multivariable models: (A) explained variation measured at 1 month and every 3 months after diagnosis, (B) smoothed local RE up to 3 years after diagnosis, for models adjusted for the effects of age and deprivation, and stage, treatment, performance status, and emergency presentation. Non‐small cell lung cancer patients diagnosed in 2012, selected for their valid stage and performance status at diagnosis: 3308 men and 2650 women. The curve for comorbidity is not presented here as it is undistinguishable from the age and deprivation model Notes: (1) RE(t) and local RE can have values between −1 and +1 (2) Cumulative RE, RE(t) is calculated at month 1, 3, 6…36 after diagnosis (3) Local RE is calculated using information from 10 events on either side of the index event. The smoothed (lowess with mean smoother) curve is presented here