First-principles modeling of electromagnetic scattering by discrete and discretely heterogeneous random media
- PMID: 29657355
- PMCID: PMC5896873
- DOI: 10.1016/j.physrep.2016.04.002
First-principles modeling of electromagnetic scattering by discrete and discretely heterogeneous random media
Abstract
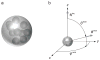
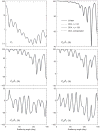
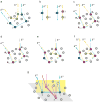
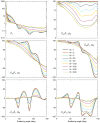
A discrete random medium is an object in the form of a finite volume of a vacuum or a homogeneous material medium filled with quasi-randomly and quasi-uniformly distributed discrete macroscopic impurities called small particles. Such objects are ubiquitous in natural and artificial environments. They are often characterized by analyzing theoretically the results of laboratory, in situ, or remote-sensing measurements of the scattering of light and other electromagnetic radiation. Electromagnetic scattering and absorption by particles can also affect the energy budget of a discrete random medium and hence various ambient physical and chemical processes. In either case electromagnetic scattering must be modeled in terms of appropriate optical observables, i.e., quadratic or bilinear forms in the field that quantify the reading of a relevant optical instrument or the electromagnetic energy budget. It is generally believed that time-harmonic Maxwell's equations can accurately describe elastic electromagnetic scattering by macroscopic particulate media that change in time much more slowly than the incident electromagnetic field. However, direct solutions of these equations for discrete random media had been impracticable until quite recently. This has led to a widespread use of various phenomenological approaches in situations when their very applicability can be questioned. Recently, however, a new branch of physical optics has emerged wherein electromagnetic scattering by discrete and discretely heterogeneous random media is modeled directly by using analytical or numerically exact computer solutions of the Maxwell equations. Therefore, the main objective of this Report is to formulate the general theoretical framework of electromagnetic scattering by discrete random media rooted in the Maxwell-Lorentz electromagnetics and discuss its immediate analytical and numerical consequences. Starting from the microscopic Maxwell-Lorentz equations, we trace the development of the first-principles formalism enabling accurate calculations of monochromatic and quasi-monochromatic scattering by static and randomly varying multiparticle groups. We illustrate how this general framework can be coupled with state-of-the-art computer solvers of the Maxwell equations and applied to direct modeling of electromagnetic scattering by representative random multi-particle groups with arbitrary packing densities. This first-principles modeling yields general physical insights unavailable with phenomenological approaches. We discuss how the first-order-scattering approximation, the radiative transfer theory, and the theory of weak localization of electromagnetic waves can be derived as immediate corollaries of the Maxwell equations for very specific and well-defined kinds of particulate medium. These recent developments confirm the mesoscopic origin of the radiative transfer, weak localization, and effective-medium regimes and help evaluate the numerical accuracy of widely used approximate modeling methodologies.
Keywords: Discrete random media; Effective-medium approximation; Electromagnetic scattering; Radiative transfer; Statistical electromagnetics; Weak localization.
Figures


















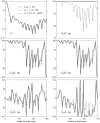
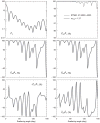
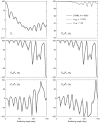


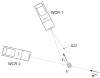




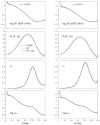


Similar articles
-
Electromagnetic scattering by spheroidal volumes of discrete random medium.J Quant Spectrosc Radiat Transf. 2017 Oct;200:244-248. doi: 10.1016/j.jqsrt.2017.06.021. Epub 2017 Jun 21. J Quant Spectrosc Radiat Transf. 2017. PMID: 29622840 Free PMC article.
-
Exact solution of Maxwell's equations for optical interactions with a macroscopic random medium.Opt Lett. 2004 Jun 15;29(12):1393-5. doi: 10.1364/ol.29.001393. Opt Lett. 2004. PMID: 15233446
-
Poynting-Stokes tensor and radiative transfer in discrete random media: the microphysical paradigm.Opt Express. 2010 Sep 13;18(19):19770-91. doi: 10.1364/OE.18.019770. Opt Express. 2010. PMID: 20940872
-
An overview of methods for deriving the radiative transfer theory from the Maxwell equations. II: Approach based on the Dyson and Bethe-Salpeter equations.J Quant Spectrosc Radiat Transf. 2019 Feb;224:25-36. doi: 10.1016/j.jqsrt.2018.10.032. Epub 2018 Oct 23. J Quant Spectrosc Radiat Transf. 2019. PMID: 30713354 Free PMC article.
-
Electromagnetic scattering and emission by a fixed multi-particle object in local thermal equilibrium: General formalism.J Quant Spectrosc Radiat Transf. 2017 Oct;200:137-145. doi: 10.1016/j.jqsrt.2017.06.003. Epub 2017 Jun 13. J Quant Spectrosc Radiat Transf. 2017. PMID: 29643568 Free PMC article.
Cited by
-
Electromagnetic scattering by spheroidal volumes of discrete random medium.J Quant Spectrosc Radiat Transf. 2017 Oct;200:244-248. doi: 10.1016/j.jqsrt.2017.06.021. Epub 2017 Jun 21. J Quant Spectrosc Radiat Transf. 2017. PMID: 29622840 Free PMC article.
-
A proof that multiple waves propagate in ensemble-averaged particulate materials.Proc Math Phys Eng Sci. 2019 Sep;475(2229):20190344. doi: 10.1098/rspa.2019.0344. Epub 2019 Sep 18. Proc Math Phys Eng Sci. 2019. PMID: 31611729 Free PMC article.
-
Light scattering in TIRF microscopy: A theoretical study of the limits to surface selectivity.Biophys J. 2021 Aug 3;120(15):2952-2968. doi: 10.1016/j.bpj.2021.06.025. Epub 2021 Jun 30. Biophys J. 2021. PMID: 34214540 Free PMC article.
-
Black carbon aerosol number and mass concentration measurements by picosecond short-range elastic backscatter lidar.Sci Rep. 2022 May 19;12(1):8443. doi: 10.1038/s41598-022-11954-7. Sci Rep. 2022. PMID: 35589746 Free PMC article.
-
Radiative transfer in a discrete random medium adjacent to a half-space with a rough interface.J Quant Spectrosc Radiat Transf. 2018 Oct;218:194-202. doi: 10.1016/j.jqsrt.2018.07.016. Epub 2018 Jun 24. J Quant Spectrosc Radiat Transf. 2018. PMID: 30504992 Free PMC article.
References
-
- van de Hulst HC. Light Scattering by Small Particles. Wiley; New York: 1957.
-
- Kerker M, editor. Electromagnetic Scattering. Macmillan; New York: 1963.
-
- Rowell RL, Stein RS, editors. Electromagnetic Scattering. Gordon and Breach; New York: 1967. - PubMed
-
- Shifrin KS. Scattering of Light in a Turbid Medium, NASA Technical Translation TT F-477. National Aeronautics and Space Administration; Washington, DC: 1968.
-
- Deirmendjian D. Electromagnetic Scattering on Spherical Polydispersions. Elsevier; New York: 1969.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
