Finite-Size Effects of Binary Mutual Diffusion Coefficients from Molecular Dynamics

Abstract

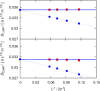
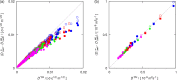
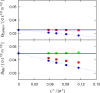
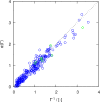
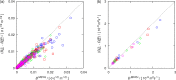
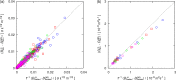
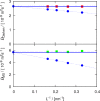
Molecular dynamics simulations were performed for the prediction of the finite-size effects of Maxwell-Stefan diffusion coefficients of molecular mixtures and a wide variety of binary Lennard-Jones systems. A strong dependency of computed diffusivities on the system size was observed. Computed diffusivities were found to increase with the number of molecules. We propose a correction for the extrapolation of Maxwell-Stefan diffusion coefficients to the thermodynamic limit, based on the study by Yeh and Hummer ( J. Phys. Chem. B , 2004 , 108 , 15873 - 15879 ). The proposed correction is a function of the viscosity of the system, the size of the simulation box, and the thermodynamic factor, which is a measure for the nonideality of the mixture. Verification is carried out for more than 200 distinct binary Lennard-Jones systems, as well as 9 binary systems of methanol, water, ethanol, acetone, methylamine, and carbon tetrachloride. Significant deviations between finite-size Maxwell-Stefan diffusivities and the corresponding diffusivities at the thermodynamic limit were found for mixtures close to demixing. In these cases, the finite-size correction can be even larger than the simulated (finite-size) Maxwell-Stefan diffusivity. Our results show that considering these finite-size effects is crucial and that the suggested correction allows for reliable computations.

Figure 1

Self-diffusion coefficients of a binary LJ mixture (x₁ = 0.9) as a function of the simulation box length (L). Blue circles are the computed self-diffusion coefficients in the finite systems, and red squares are the corrected values using the YH correction term (eq 2). The dashed lines indicate extrapolation to the thermodynamic limit, and the solid lines show the extrapolated self-diffusivities. The second component has ϵ₂ = 0.5 × ϵ₁ and σ₂ = 1.2 × σ₁, and the adjustable parameter (k_ij) to the Lorentz–Berthelot mixing rules is 0. The error bars are smaller than the symbols.

Figure 2

Finite-size corrections required for self-diffusion coefficients as a function of the YH correction (D^YH, Equation 2) for (a) LJ and (b) molecular mixtures computed with 500 LJ particles/250 molecules (blue circles), 1000 LJ particles/500 molecules (red squares), 2000 LJ particles/1000 molecules (green diamonds), and 4000 LJ particles/2000 molecules (magenta pentagons). Closed and open symbols represent the corrections to the self-diffusivity of species 1 and species 2, respectively. The dashed lines indicate perfect agreement. Statistical uncertainties are listed in the Supporting Information.

Figure 3

Diffusion coefficients of a binary LJ mixture (x₁ = 0.9) as a function of the simulation box length (L). Blue circles are the computed Darken (eq 10) and MS (eq 8) diffusivities. Red and green squares are the corrected values according to the YH (eq 2) and the MSYH (eq 17), respectively. The dashed lines show extrapolation to the thermodynamic limit, and the solid lines show the extrapolated values. The second component has ϵ₂ = 0.5 × ϵ₁ and σ₂ = 1.2 × σ₁, and the adjustment parameter (k_ij) to the Lorentz–Berthelot mixing rules is 0. The error bars are smaller than the symbols.

Figure 4

Modification factor to the YH correction (α) as a function of the thermodynamic factor (Γ) for nonideal mixtures according to eq 16. Blue circles and green diamonds show the modification factors for the LJ and molecular systems, respectively. The thermodynamic factor for ideal mixtures equals 1. The dashed line indicates perfect agreement. Statistical uncertainties are listed in the Supporting Information.

Figure 5

Correction needed for the MS diffusion coefficients versus the MSYH correction term (Đ^MSYH, eq 17) for (a) LJ and (b) molecular systems computed with 500 LJ particles/250 molecules (blue circles), 1000 LJ particles/500 molecules (red squares), 2000 LJ particles/1000 molecules (green diamonds), and 4000 LJ particles/2000 molecules (magenta pentagons). The dashed lines show perfect agreement. The statistical uncertainties are listed in the Supporting Information.

Figure 6

Correction needed for the MS diffusion coefficients versus the extrapolated Darken equation with the modification factor included (Γ^–1(Đ_Darken^∞ – Đ_Darken^MD)) for (a) LJ and (b) molecular systems computed with 500 LJ particles/250 molecules (blue circles), 1000 LJ particles/500 molecules (red squares), 2000 LJ particles/1000 molecules (green diamonds), and 4000 LJ particles/2000 molecules (magenta pentagons). The dashed lines show perfect agreement. The statistical uncertainties are listed in the Supporting Information.

Figure 7

Binary Darken (Equation 10) and MS (Equation 8) diffusivities for a mixture of methanol–carbon tetrachloride (x_methanol = 0.9) as a function of the simulation box (L). Blue circles are the computed diffusion coefficients in MD simulations. Red and green squares are the corrected diffusivities according to the YH (Equation 2) and MSYH (eq 17) corrections, respectively. Dashed lines show extrapolation to the thermodynamic limit, and solid lines are the extrapolated values.