Renewing Felsenstein's phylogenetic bootstrap in the era of big data
- PMID: 29670290
- PMCID: PMC6030568
- DOI: 10.1038/s41586-018-0043-0
Renewing Felsenstein's phylogenetic bootstrap in the era of big data
Abstract
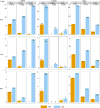
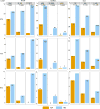
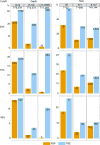
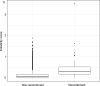
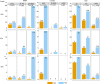
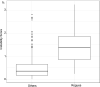
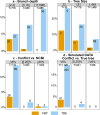
Felsenstein's application of the bootstrap method to evolutionary trees is one of the most cited scientific papers of all time. The bootstrap method, which is based on resampling and replications, is used extensively to assess the robustness of phylogenetic inferences. However, increasing numbers of sequences are now available for a wide variety of species, and phylogenies based on hundreds or thousands of taxa are becoming routine. With phylogenies of this size Felsenstein's bootstrap tends to yield very low supports, especially on deep branches. Here we propose a new version of the phylogenetic bootstrap in which the presence of inferred branches in replications is measured using a gradual 'transfer' distance rather than the binary presence or absence index used in Felsenstein's original version. The resulting supports are higher and do not induce falsely supported branches. The application of our method to large mammal, HIV and simulated datasets reveals their phylogenetic signals, whereas Felsenstein's bootstrap fails to do so.
Conflict of interest statement
Figures







References
-
- Efron B. Bootstrap Methods: Another Look at the Jackknife. Ann. Stat. 1979;7:1–26.
-
- Efron B, Tibshirani RJ. An introduction to the bootstrap. Chapman & Hall, NY; 1993.
-
- Felsenstein J. Confidence limits on phylogenies: an approach using the bootstrap. Evolution. 1985;39:783–791. - PubMed
-
- Van Noorden R, Maher B, Nuzzo R. The top 100 papers. Nature. 2014;514:550–553. - PubMed
-
- Sanderson MJ. Objections to bootstrapping phylogenies: A critique. Syst. Biol. 1995;44:299–320.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

